Hom ho expressa amb
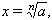
on a és el subradicand, x l’arrel i n l’índex; aquesta expressió equival a xn = a. El signe √sembla provenir de la deformació de la r inicial del mot llatí radix, ‘arrel’ (àlgebra). Una arrel d’índex 2 és anomenada arrel quadrada hom acostuma a suprimir gràficament l’índex; d’índex 3, arrel cúbica; d’índex 4, arrel biquadrada. Les arrels de qualsevol altre índex no reben cap nom específic. L’existència d’una arrel enèsima (d’índex n) q de p, on q i p són nombres reals i positius, és demostrada pel fet que la funció y = xn, on x varia de 0 a + ∞, és contínua i, per tant, pot abastar tots els valors reals positius. Tot nombre real i positiu admet dues arrels d’índex parell que són dos nombres reals oposats i una sola d’índex imparell. Tot nombre real i negatiu admet una arrel real única d’índex imparell i cap arrel d’índex parell. Hom acostuma a emprar també la notació equivalent següent:
 i aleshores el càlcul d’arrels queda reduït al càlcul de potències. Per a les arrels quadrades, cúbiques i biquadrades hom ha desenvolupat tècniques matemàtiques adequades per a resoldre-les. Per a un índex n qualsevol, hom pren logaritmes, així,
i aleshores el càlcul d’arrels queda reduït al càlcul de potències. Per a les arrels quadrades, cúbiques i biquadrades hom ha desenvolupat tècniques matemàtiques adequades per a resoldre-les. Per a un índex n qualsevol, hom pren logaritmes, així,
 és equivalent a
és equivalent a
 i aleshores
i aleshores
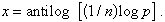 Les principals propietats de la radicació són les següents: arrel d’una potència:
Les principals propietats de la radicació són les següents: arrel d’una potència:
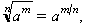 producte d’arrels d’índex igual:
producte d’arrels d’índex igual:
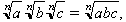

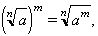
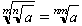

 i d’arguments respectius
i d’arguments respectius




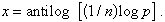
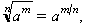
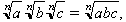
quocient d’arrels d’índex igual:

potència d’una arrel:
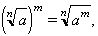
arrel d’una altra arrel:
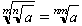
producte d’arrels d’índex diferent:

Un nombre complex p pot ésser considerat com la suma p = a + b i, amb a b reals i a més p = (cos ø + sin ø), on p és el mòdul i ø l’argument de p. Aleshores p tindrà n arrels enèsimes (d’índex n) amb mòdul igual


i els afixos d’aquestes arrels determinaran al pla d’Argand-Gauss un polígon de n costats.