La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P ( x,y ) d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents:
sin α = y/r (sinus)
cos α = x/r (cosinus)
tg α = y/x (tangent)
cotg α x/y (cotangent)
sec α = r/x (secant)
cosec α = r/y (cosecant)
Quan el punt P
és a una distància r
= 1 de l’origen O
, el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats
línies trigonomètriques (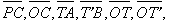
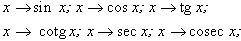
, respectivament), fàcils de traçar. A partir de cadascuna d’aquestes raons, hom defineix una funció real de variables reals que té el mateix nom que la raó corresponent: x
és interpretada habitualment com la mesura d’un angle en radiants. Aquestes funcions, anomenades funcions trigonomètriques
o circulars
, són periòdiques i de període 2π. Les més utilitzades són el sinus, el cosinus i la tangent. Les relacions inverses, restringides a dominis convenients, són unes noves funcions, anomenades funcions trigonomètriques inverses
, el domini i simbolismes de les més importants de les quals són els següents:
on
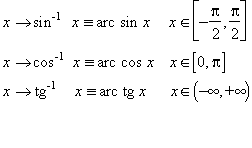
Les equacions on hi ha expressions trigonomètriques són anomenades equacions trigonomètriques . Totes les raons trigonomètriques d’un angle resten determinades, a part el signe, pel coneixement d’una d’elles, tal com resulta de les relacions següents:
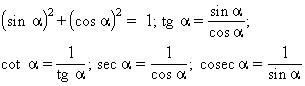
que, d’altra banda, són una conseqüència immediata de les corresponents definicions. Les raons trigonomètriques dels angles dels quatre quadrants poden ésser expressades a partir de les dels angles del primer quadrant, fent servir les relacions:
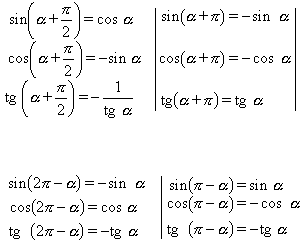
que són evidents a partir de les definicions; les raons dels angles complementaris es relacionen per
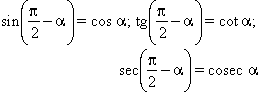
De tot això, en resulta que les raons trigonomètriques de qualsevol angle poden ésser determinades coneixent únicament el valor d’una raó dels angles compresos entre 0 i π/4. Aquesta mínima informació, a vegades ampliada per comoditat fins a π/2 i amb l’addició supèrflua dels valors de les altres raons trigonomètriques, és continguda en les anomenades taules trigonomètriques naturals , les quals hom troba disponibles en nombrosos formats i amb una aproximació que oscil·la entre 4 i 20 xifres decimals. Les funcions trigonomètriques no són morfismes respecte a la suma a ℝ, sinó que compleixen les relacions:
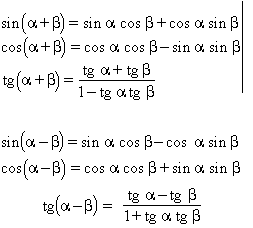
d’on resulta
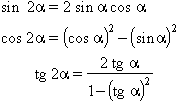
i també
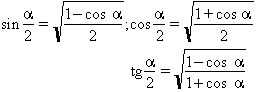
com també les següents relacions, molt útils:
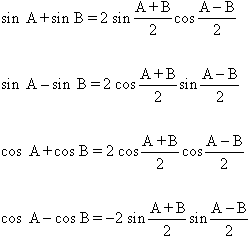
Els problemes clàssics de la trigonometria són els de la resolució de triangles , consistents a determinar les longituds dels costats i les amplituds dels angles de qualsevol triangle a partir d’una informació mínima (3 costats, 2 costats i angle, o bé 1 costat i 2 angles), suficient per a fer-ho. La resolució dels triangles es basa en dos teoremes, el dels sinus i el dels cosinus. Segons el teorema dels sinus , en tot triangle es compleix que
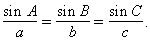
Segons el teorema del cosinus , en tot triangle es compleixen les relacions:
a 2 = b 2 + c 2 - 2 bc cos A
b 2 = c 2 + a 2 - 2 ca cos B
c 2 = a 2 + b 2 - 2 ab cos C
Una modificació i generalització de la trigonometria plana descrita és la trigonometria esfèrica , dedicada a l’estudi de les relacions entre les amplituds dels angles i les amplituds dels costats dels triangles esfèrics ; té un gran interès en astronomia, geodèsia i nàutica. Les fórmules corresponents als teoremes del sinus i del cosinus de la trigonometria plana i que permeten la resolució dels triangles esfèrics són les fórmules conegudes com a grup de Bessel. També són utilitzades altres fórmules, com les analogies de Neper i de Delambre.
Històricament, sembla que la trigonometria començà amb l’intent d’Hiparc d’utilitzar, per a caracteritzar els angles, la longitud de la corda corresponent en el cercle de radi unitat. Al s VI el matemàtic indi Āryabhata utilitzà la meitat de la longitud de la corda de l’angle doble (el que avui hom anomena sinus ). D’altra banda, Menelau, astrònom d’Alexandria, escriví el tractat Esfèrica , on estudià sistemàticament la trigonometria esfèrica, a les acaballes del s I. Bé que sense utilitzar el sinus, a l’obra Almagest de Ptolemeu hi ha ja una bona col·lecció de resultats trigonomètrics. Els àrabs, reunint els coneixements hel·lenístics amb la descoberta hindú dels sinus, elaboraren les primeres taules trigonomètriques, alhora que descobriren les relacions elementals entre les raons. Tot això passà a l’Occident cristià a través de les penínsules Ibèrica i Itàlica, i contribuí al desenvolupament de les tècniques de navegació. L’any 1553 Regiomontanus publicà a Nuremberg De triangulis omnimodis libri quinque , obra molt influent, en la qual, entre d’altres novetats, apareix per primera vegada el teorema que avui és anomenat dels sinus , alhora que hi ha també les primeres idees sobre cosinus i tangents. Més tard, Viète posà la trigonometria a l’abast de la tècnica, en estudiar les conseqüències de les divisions dels arcs i en facilitar la construcció de taules trigonomètriques detallades (Burgui, Van Romen), cap al 1600. En la trigonometria esfèrica, Viète mateix descobrí i sistematitzà les anomenades analogies de Neper , que ajuden a la resolució dels triangles. A poc a poc la trigonometria anà adquirint la forma que avui té, i l’estudi de les funcions trigonomètriques rebé un bon impuls gràcies a Euler (1730) quan, utilitzant els nombres complexos, aconseguí de relacionar les funcions trigonomètriques amb les exponencials i les logarítmiques.