Fill d’un astrònom, hom el suposa parent del tirà de Siracusa, Hieró. Fou mort per un soldat romà quan les tropes de Marcel saquejaren Siracusa en el curs de la segona guerra Púnica. És difícil de destriar la veritat de la llegenda en els altres detalls de la seva biografia. Es destacà en geometria pura. Havia estudiat Euclides i tingué alguna relació amb Eratòstenes. Hom li pot suposar, però, una certa oposició enfront de la ciència oficial de l’època detinguda pels professors que residien a Alexandria, atesos la profunda originalitat de la seva obra científica, el dialecte dòric en què fou escrita i la molta feina d’enginyer que probablement dugué a terme.
Entre les obres matemàtiques que n'han pervingut convé d’esmentar De l’esfera i el cilindre, La mesura del cercle, Dels esferoides i els conoides i De les línies espirals. El descobriment més important fou, fins i tot per al mateix Arquimedes, la demostració que l’àrea de l’esfera és igual a l’àrea lateral del cilindre recte circumscrit i que l’àrea total d’aquest cilindre i el seu volum són, ambdós, una vegada i mitja els respectius de l’esfera.
En La mesura del cercle demostrà que l’àrea del cercle és igual a la d’un triangle rectangle els catets del quals siguin, respectivament, iguals al radi i a la longitud de la circumferència. El problema, aleshores, es redueix a calcular la relació de la circumferència amb el diàmetre (nombre π). Malgrat les dificultats que presentava el sistema de numeració alfabètic dels grecs, Arquimedes demostra ésser un mestre en el càlcul numèric, i amb els polígons inscrit i circumscrit de 96 costats arribà a la conclusió de limitar π per la doble desigualtat
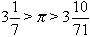
que dona un error comprès entre +0,0016 i -0,0008. Autors posteriors li han atribuït un resultat que equival a donar quatre xifres decimals exactes.
Entre les obres de mecànica convé de subratllar De l’equilibri dels plans i Dels cossos flotants, en dos volums cadascuna. En el primer llibre de la primera establí els principis fonamentals de l’estàtica, i és particularment famós per la llei de la palanca. Més endavant trobà els centres de gravetat de certs polígons, i, ja en el llibre segon, els de diverses àrees parabòliques. En relació amb aquests treballs d’estàtica és atribuïda a Arquimedes la frase de “Doneu-me un punt (per fulcre) i (amb una palanca) soc capaç de moure el món”. Per contra, és versemblant que dotà el port de Siracusa de ginys portuaris, que després, durant el setge, foren transformats en màquines bèl·liques.
En el tractat Dels cossos flotants establí, primer, que la superfície d’un fluid en repòs és una esfera que té per centre el de la Terra; demostrà, després, la llei física coneguda com el principi d'Arquimedes. Trobà també la posició de repòs i les condicions de l’estabilitat d’un segment d’esfera i d’un segment de paraboloide.
En l'Arenari, una de les seves obres menors, construí un sistema de numeració que permet d’expressar quantitats més grans que qualsevol de les que hom pugui trobar en la pràctica.
En el Mètode explicà a Eratòstenes com havia trobat molts dels seus resultats a base d’una comparació mecànica, de fet molt semblant a la idea fonamental del càlcul integral. Arquimedes cregué, això no obstant, que aquest mètode només era bo per a intuir els resultats, els quals no podien ésser considerats vàlids fins haver-ne trobat una demostració geomètrica. Això és el que feu en la seva obra La quadratura de la paràbola seguint l’enginyós camí de l’exhaustió, que consisteix a esgotar el segment parabòlic llevant-li àrees finites que són cada vegada més petites. Hom li atribueix també el Problema dels bous, en el qual es planteja una qüestió, aparentment simple, d’anàlisi diofàntica que no pot ésser resolta sinó per nombres fabulosament elevats. Entre les obres considerades perdudes hom cita la Catròptica i De la construcció d’esferes.
Fora de les obres escrites, hom atribueix a Arquimedes la resolució de l’anomenat “problema de la corona”. Sembla que Hieró encarregà una corona que pagà com si fos d’or fi i que després temé que podia ésser d’or lligat amb argent. Arquimedes resolgué el problema determinant el volum de la corona submergint-la en un recipient completament ple i pesant l’aigua vessada; així trobà la densitat de la corona i pogué calcular el percentatge d’argent que hi havia posat el joier infidel. Hom diu que Arquimedes pensà aquest procediment quan ell mateix vessà aigua en ficar-se en una banyera massa plena i que en va sortir bo i cridant eureka! (η'ýρηκα, ‘ho he trobat’) Tots els autors antics atorguen a Arquimedes el mèrit de les màquines de guerra gràcies a les quals la ciutat de Siracusa pogué resistir un perllongat setge dels romans. És palesament fals, per contra, que Arquimedes fes construir uns miralls gegantins (els llegendaris miralls ustoris) amb l’ajuda dels quals hauria concentrat els raigs del sol per tal d’incendiar les naus romanes.