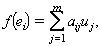I acomplint-se les propietats (λ + μ) e = λ e + μ e , λ( e + f ) = λ e + λ f , λ(μ e ) = (λμ) e i 1 e = e . Els elements de E són anomenats vectors , i els elements de K , escalars . Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial. Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F . Això permet de formar el conjunt quocient E/F (quocient), el qual, definint la suma x + y = x + y i el producte per escalars λ x = λ x , es converteix en un nou espai vectorial dit espai quocient de E pel subespai F . Tot vector de E que hom pugui expressar en la forma x = λ 1 ν 1 + λ 2 ν 2 + ... + λ k ν k és anomenat combinació lineal dels vectors ν 1 , ..., ν k , i forma un subespai vectorial de E anomenat subespai generat o engendrat pels vectors ν 1 , ν 2 ,...,ν k , dits també generadors del subespai . Un sistema de vectors {ν i }, i∈I , és anomenat linealment independent si les úniques combinacions lineals dels seus elements, que són zero, són les que tenen tots els coeficients igualats a zero. Un conjunt de generadors de l’espai E que siguin linealment independents rep el nom de base. Es demostra que tot espai vectorial admet una base i que totes les bases d’un espai vectorial tenen el mateix cardinal, i en particular, si són finites, totes tenen el mateix nombre d’elements. Aquest nombre és la dimensió de l’espai. Tot vector pot ésser expressat en funció de la base en forma de combinació lineal i l’expressió és única. Els coeficients que formen part de la combinació lineal són les components del vector en la base donada. Si E i F són dos espais vectorials, una aplicació f:E → F és anomenada lineal o morfisme si verifica f ( x + y ) = f ( x ) + f ( y ), f (λ x ) = λ f ( x ) per a tot x,y de E i tot λ de K . El conjunt d’elements de E que tenen imatge nul·la en l’aplicació és anomenat nucli del morfisme f (Nuc f , o Ker f ) i és un subespai de E ; el conjunt d’elements de F que són imatge d’algun element de E és anomenat imatge de f (Im f ) i és un subespai de F . Es verifica que el quocient de E pel nucli del morfisme és isomorf a la imatge. En el cas que E i F siguin de dimensió finita, les imatges dels vectors d’una base e 1 ,..., e n de E generen Im f , la dimensió de Im f que és el nombre de vectors f ( e 1 ),..., f ( e n ) linealment independents és anomenada rang de l’aplicació lineal. Expressant els vectors f ( e i ) en una base ν 1 ,...,ν m de F hom obté fórmules del tipus