Resulta d’expressar l’equació de Laplace, ∇2ψ(x, y, z) = 0, en coordenades cilíndriquesquan és possible d’aplicar a la funció ϕ el mètode de separació de variables: ϕ x,y,z) = X(x)Y(y)Z(z). Una sol·lució particular de l’equació de Bessel és la funció de Bessel de primera classe, d’ordre ν:
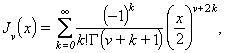
on Γ és la funció gamma. J-ν (x) n'és també solució particular. Si n és enter, la corresponent funció Jn(x) pot ésser estesa a tot ℂ; si ν no és enter, Jν (x) pot ésser estesa a ℂllevat de l’eix real negatiu. Si n és enter, J-n(x) = (-1)nJn(x); en canvi, si ν no és enter, Jν(x) i J-ν(x) són independents, de manera que, en aquest cas, la solució general de l’equació de Bessel és y(x) = aJν(x) + bJ-ν(x), essent a i b constants ajustables. Hom defineix les funcions de Bessel de segona classe o funcions de Neumann, d’ordre ν, de la manera següent: si ν no és enter, aleshores és:
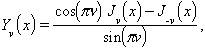
i si n és enter, aleshores
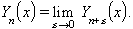
Per a tot ν, Yνés solució de l’equació de Bessel. Si n és enter, Jni Ynsón independents, de manera que, en aquest cas, la solució general és y(x)=aJν(x)+bYν (x). Hom anomena funcions de Bessel de tercera classe o funcions de Hankel d’ordre ν,
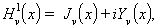
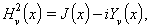
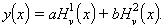
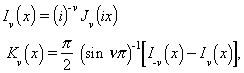
essent
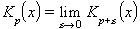
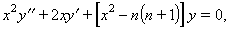
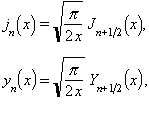
anomenades funcions esfèriques de Bessel de la 2a classe, d’ordre n.