El primer estudi conegut sobre còniques és el tractat d’Apol·loni de Perge, que les definia com a possibles seccions d’un con. Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat. L’estudi afí de les còniques destaca els següents elements: centre, que és el pol de la recta de l’infinit, diàmetre, qualsevol recta que passa pel centre, asímptotes, els diàmetres tangents a la cònica.
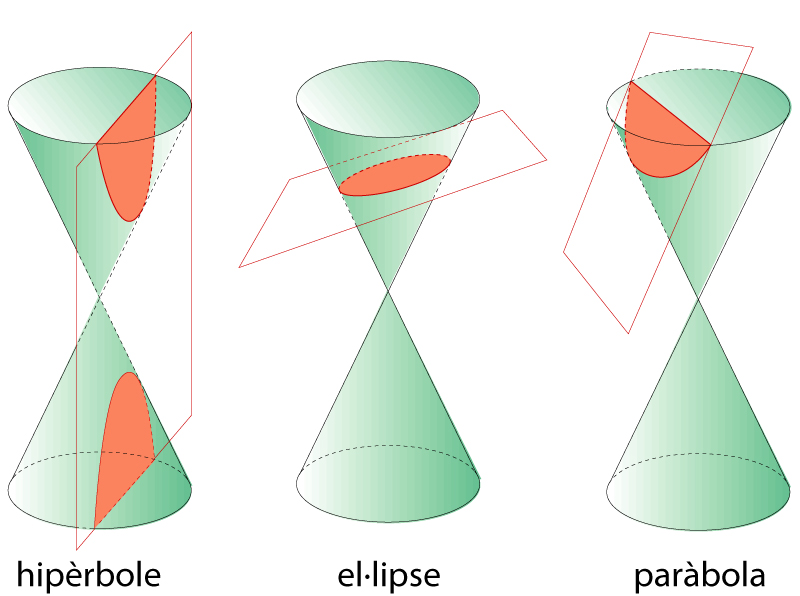
En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la cònica. Els focus són aquells punts en què, en el feix de rectes incident, coincideixen la involució de rectes perpendiculars i la induïda per la cònica. La intersecció d’una cònica amb un eix és anomenada vèrtex. La classificació projectiva de les còniques només distingeix entre pròpies o degenerades (rang 3 o inferior) i reals o imaginàries (índex 1 o 0). La intersecció de les còniques reals no degenerades amb la recta de l’infinit fa la distinció afí : intersecció dos punts, hipèrbola; un punt, paràbola; i si no hi ha intersecció, el·lipse.
En sistemes de referència centrals, les equacions reduïdes serien: el·lipse (x2 / a2) + (y2 / b2) = 1 (si a = b, circumferència), hipèrbola (x2 / a2) — (y2 / b2) = 1, i paràbola y2 = 2 px (en el cas de la paràbola, el sistema de referència que dona aquesta equació reduïda té centre en un vèrtex).