El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier. Tota funció periòdica f(x), contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera:
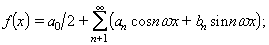
la sèrie que apareix en aquesta expressió és la sèrie de Fourier de (o associada a) la funció f(x). El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació (o freqüència angular) de f, és a dir, ω=2π/T, on T és el període de f. El primer terme de la sèrie de Fourier de f, terme que correspon al valor n=1 de l’índex de sumatori, és anomenat harmònic fonamental (o primer harmònic o harmònic d’ordre 1); els altres termes són els seus harmònics (els harmònics del fonamental); per exemple, el terme que correspon al valor n=k de l’índex del sumatori és el k-èsim harmònic o harmònic d’ordre k. Tots els harmònics admeten una expressió sinusoidal; per exemple, el n-èsim harmònic pot escriure's en la forma ancosnωx+ bnsinnϖx = rncos(nωx+φn), on rn, φn, nω i nω/2 són anomenats, respectivament, l'amplitud, la fase, la pulsació (o freqüència angular) i la freqüència del n-èsim harmònic. Així, doncs, les freqüències dels harmònics són múltiples de la freqüència de l’harmònic fonamental, i hom parla, en considerar les freqüències, de la freqüència fonamental i dels seus harmònics. Els nombres ani bnde la sèrie de Fourier de f són els coeficients de Fourier de f. La determinació d’aquests coeficients, que configura l’anomenada anàlisi harmònica de la funció f, és assolida mitjançant les expressions
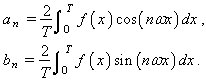
Si f és una funció parella, tots els coeficients bnsón nuls, i si és imparella ho són els an. Mitjançant l’expressió exponencial de les funcions trigonomètriques, la funció f admet l’expressió
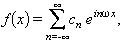
que és la forma complexa de la sèrie de Fourier. Els coeficients de Fourier són donats ara per l’expressió
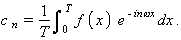
Hom pot generalitzar aquests resultats en el cas que la funció f no és periòdica. En efecte, sota condicions bastant generals de continuïtat, una funció f(x) admet l’expressió
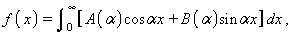
anomenada integral de Fourier, en la qual els coeficients són
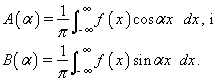
L’expressió exponencial de les funcions trigonomètriques permet de fer
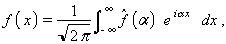
on f(α) és la transformada de Fourier de la funció f(x), que és donada per l’expressió
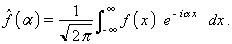
L’aplicació que assigna a cada funció f la seva transformada de Fourier f és anomenada transformació de Fourier. L’anàlisi de Fourier té una importància rellevant a l’hora d’estudiar fenòmens ondulatoris, en òptica, termodinàmica, mecànica quàntica, etc.