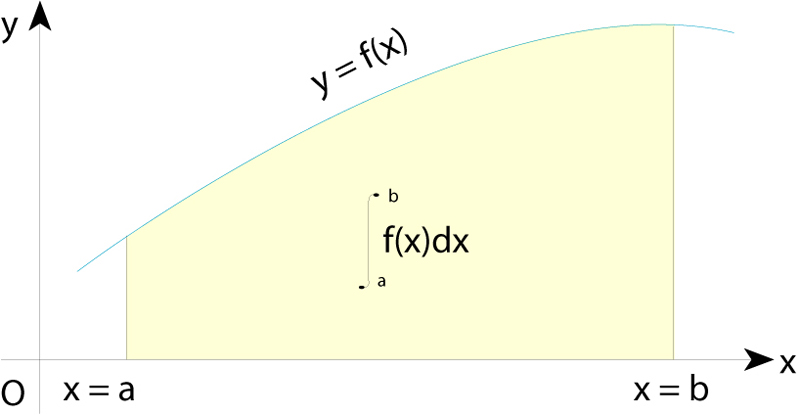
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann, la integral de Riemann-Stieltjes i la integral de Lebesgue . La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques. Si [a,b] és un interval tancat de la recta real, i P={ x0,..., xn } és una partició de [a,b], és a dir, un conjunt finit de punts tal que a = x0 ≤ x1 ≤... ≤ xn = b, sigui Δ xi = xi-1 per a i =1,..., n . Si f és una funció fitada definida en [a, b], hom determina en cada subinterval [ xi-1, xi ] els termes Mi =sup f (x) i mi =inf f (x), és a dir, el màxim i el mínim de f (x) en aquest subinterval; hom defineix les sumes parcials superior i inferior per
els nombres
on m i i M i són iguals als definits en el cas de la integral de Riemann; els nombres
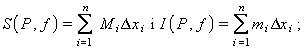
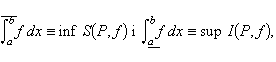
en què el màxim (sup) i el mínim (inf) de les sumes parcials són determinats en fer totes les possibles particions de l’interval original [a,b], són anomenats integral de Riemann superior i integral de Riemann inferior, respectivament, de f en [a,b]. Si aquests dos termes són iguals, hom diu que la funció f és integrable en el sentit de Riemann en [a,b], i llur valor comú és anomenat integral de Riemann de f en [a,b] i és notat per ∫ b a f dx o per ∫ b a f (x) dx. En aquesta integral, f és l’integrant i a i b són el límit superior d’integració i el límit inferior d’integració, respectivament. La integral així definida és l’emprada, generalment, en el càlcul integral elemental, per la qual cosa hom parla, simplement de la integral de f en [a,b] o de la integral definida de f en [a,b], sense especificar que es tracta de la integral de Riemann. Aquesta integral té dues interpretacions força interessants. D’una banda, admet una interpretació geomètrica simple; en efecte, la integral ∫ b a f dx dona l’àrea limitada per la gràfica de la funció f i l’eix d’abscisses, entre els punts a i b d’aquest. D’altra banda, permet de generar, a partir del concepte d’integral indefinida, les primitives d’una funció (funció primitiva), de manera que la integral, entesa com a operació sobre funcions, realitza un paper invers al de la derivada. Juntament amb el concepte de funció, límit i continuïtat, aquests dos conceptes, derivada i integral, constitueixen el bastiment de l’anàlisi matemàtica.
Un tipus més general d’integral és l’anomenada integral de Riemann-Stieltjes, que es defineix d’una manera anàloga. Sigui [a,b] un interval tancat de la recta real i sigui α una funció estrictament creixent en [a,b]. Per a cada partició P de [a,b] hom defineix el terme Δαi =α(xi) —α(xi-1) ≥0. Si f és una funció fitada definida en [a,b], hom determina els termes
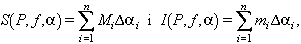
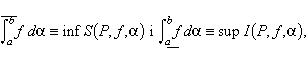
en què el màxim (sup) i el mínim (inf) de les sumes parcials són determinats en fer totes les possibles particions de l’interval original [a,b], són anomenats integral de Riemann-Stieltjes, superior i inferior, respectivament, de f en [a,b]. Si aquests dos termes són iguals, hom diu que la funció f és integrable en el sentit de Riemann respecte a α en [a,b], i llur valor comú és anomenat integral de Riemann de f respecte a α en [a,b], i és notat per ∫ b a f d α o per ∫ b a f (x) dα (x). D’aquí resulta que la integral de Riemann abans definida és el cas particular α(x) ≡; x de la integral de Riemann-Stieltjes.
La integral de Lebesgue requereix, per tal de definir-la correctament, d’emprar un espai mesurable i una mesura, convenientment definida. La integral fins aquí definida és també anomenada integral simple per tal com dona peu al càlcul de la integral múltiple (integral doble, triple, etc.) i de les integrals de línia, de superfície i de volum.