És una funció periòdica de període 2 i el seu recorregut és (-∞, ∞). És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =(sin x )/(cos x ). És indefinidament derivable i el seu desenvolupament en sèrie entera és
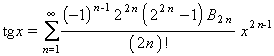
quan x 2 2 /4, i on B 2 n és l’enèsim nombre de Bernoulli (nombres de Bernoulli). En termes de la funció exponencial complexa té l’expressió
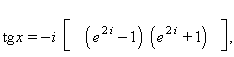
relació que permet estendre-la al cos dels nombres complexos, resultant-ne la funció tangent complexa.