Resultats de la cerca
Es mostren 13 resultats
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de…
Jean Baptiste Joseph Fourier
Matemàtiques
Matemàtic francès.
Fou professor d’anàlisi matemàtica a l’École Polytechnique 1795 de París Estudià la propagació de la calor, i publicà Théorie analytique de la chaleur 1822 Fruit d’aquest treball fou el desenvolupament de les sèries matemàtiques que duen el seu nom i que constitueixen la base de l’anàlisi harmònica anàlisi de Fourier Fou nomenat secretari perpetu de l’Académie des Sciences el 1822 i membre de l’Académie Française el 1826
convolució
Matemàtiques
Donades dues funcions reals de variable real, f(x) i g(x), funció definida per la integral: .
La convolució, o producte de convolució , té les propietats commutativa, associativa i distributiva Hi ha dos teoremes importants sobre la convolució El primer, o teorema de Parseval , afirma que la transformada de Laplace o de Fourier de la convolució de dues funcions és el producte de les transformades de Laplace o Fourier, respectivament, de les dues funcions F f*g y = Ff y x Fg y Segons el segon, la transformada de Fourier del producte de dues funcions és igual a la convolució de les seves transformades dividit per 2π F f x g y = 1/2π Ff…
desenvolupament en sèrie
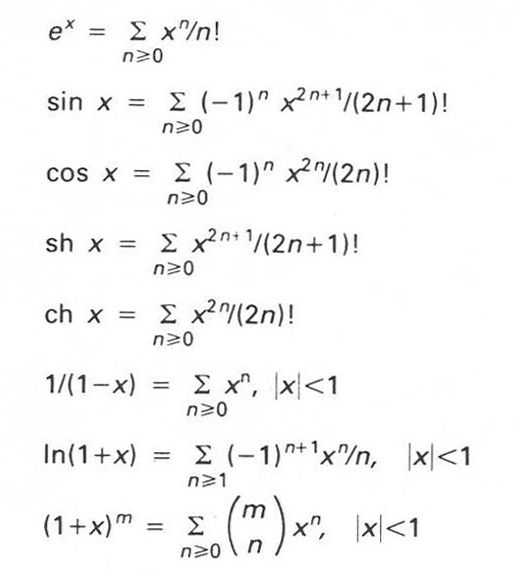
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
transformació integral
Matemàtiques
Operació mitjançant la qual una funció f(x) és transformada en una altra funció F(y) gràcies a relacions de tipus integral.
L’exemple més senzill és la simple integració F y = ∫ a y f x dx Una expressió vàlida per a un nombre important de transformacions integrals és F y = ∫ a b K x,y f x dx en la qual K x,y rep el nom de nucli i caracteritza l’esmentada transformació en molts casos, els límits d’integració són 0, ∞ i -∞, ∞ Cal esmentar, com a exemples importants, la integral ponderada, la integral de convolució, la transformada de Fourier anàlisi de Fourier, la de Laplace, la de Kankel, i la de Mellin
harmònic
Física
Matemàtiques
Cadascun dels termes de la sèrie de Fourier d’una funció periòdica (anàlisi de Fourier).
El terme de la sèrie de freqüència més baixa és anomenat harmònic fonamental o primer harmònic , i els altres termes són anomenats harmònics del fonamental
teorema de Riesz-Fischer
Matemàtiques
Teorema segons el qual l’espai ℒ2 de funcions de quadrat integrable respecte a una mesura m (f:Ω →ℂ, ∫|f|2dm< ∞) és un espai complet.
És un resultat bàsic en l’anàlisi de Fourier
transformada
Física
Matemàtiques
Dit d’una funció matemàtica definida mitjançant una operació en què intervé la funció que hom vol transformar, la qual cosa facilita la resolució numèrica de determinades aplicacions pràctiques.
En són exemples la transformada de Fourier, la transformada de Laplace i la transformada de Carson transformació
filtratge
Matemàtiques
Mètode numèric per a estimar el valor real d’una magnitud a partir del valor d’una mesura seva.
La diferència entre ambdós valors és anomenada soroll i, per hipòtesi, és una variable aleatòria Entre els mètodes de filtratge hom distingeix els lineals mínims quadrats, mitjanes mòbils i allisatge exponencial i els no lineals mètode de Fourier, de la transformació en z i de Kalman Té aplicació en la predicció i en la previsió
Norbert Wiener
Matemàtiques
Matemàtic nord-americà.
Estudià a Harvard, Cambridge i Göttingen Fou nomenat professor de lògica matemàtica al MIT 1932 Hom el considera el creador de la cibernètica , les bases de la qual exposà en l’obra Cybernetics 1948, les quals han donat lloc posteriorment a un gran nombre d’aplicacions Poc després publicà Human Use of Human Beings Cybernetics and Society 1950, que ha estat traduïda al català Cibernètica i Societat , 1969, i I am a Mathematician 1956 Són notables, també, les seves recerques sobre teoria de probabilitats, integrals de Fourier, anàlisi harmònica, espais vectorials, moviment brownià…