Resultats de la cerca
Es mostren 8 resultats
múltiple
Matemàtiques
Donat un nombre enter n, nombre m tal, que m = an, on a és també enter.
Una definició anàloga serveix per als polinomis
grup topològic
Matemàtiques
Conjunt que és alhora un grup i un espai topològic, de manera que totes dues estructures són compatibles, és a dir, que l’operació de grup i l’aplicació que assigna a cada element el seu invers són contínues.
D’una manera anàloga hom defineix els anells, els cossos o els espais vectorials topològics
submúltiple
Matemàtiques
Donat un nombre enter n, nombre m tal, que m = n/a, on a és també enter.
Una definició anàloga pot ésser feta per a polinomis Els submúltiples decimals d’una quantitat són les quantitats que resulten de multiplicar-la per potències negatives de deu
Zenodor
Matemàtiques
Matemàtic grec de l’escola d’Alexandria.
Comparà les superfícies dels polígons isoperímetres i arribà a la conclusió que el cercle és el que enclou l’àrea màxima arribà també a una conclusió anàloga pel que fa a l’esfera
teoria de les fluxions
Física
Matemàtiques
Teoria desenvolupada per I.Newton que constitueix el precedent més immediat de la teoria de derivades.
Fou utilitzada per ell mateix per a fer els càlculs astronòmics destinats a comprovar la validesa de les lleis de la mecànica que havia enunciat Els seguidors de Newton a Anglaterra i els deixebles de Leibniz a l’Europa continental sostingueren una controvèrsia, a conseqüència de la qual hom arribà a formular una teoria anàloga a la de les fluxions, però amb una notació diferent, que és la utilitzada encara actualment anàlisi matemàtica
teoria de nombres
Matemàtiques
Part de la matemàtica que estudia les relacions entre els nombres enters.
En la història de la teoria de nombres hom pot assenyalar dos grans períodes un que va des d’Euclides fins a Hilbert, i un altre que comença a partir de Hilbert Els primers tractats de teoria de nombres es troben en els Elements d’Euclides i en l' Aritmètica de Diofant d’Alexandria, i tracten, respectivament, de la divisibilitat en els racionals enters i de l’obtenció de solucions racionals i enteres d’algunes equacions algèbriques La figura més coneguda d’aquesta primera etapa és la del matemàtic francès Pierre de Fermat 1601-65, que conjecturà el famós gran teorema de Fermat encara avui no…
integral
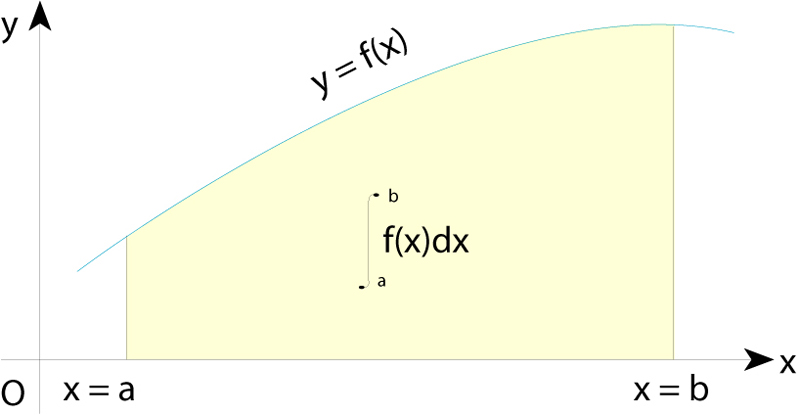
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i els termes M i…
matriu
Matemàtiques
Disposició dels elements d’un cos K
de la manera següent
.
Segons que el cos K sigui el dels nombres reals o el dels nombres complexos, hom parla de matriu real o de matriu complexa , respectivament Cadascuna de les línies horitzontals de nombres és una fila de la matriu, i cada línia vertical de nombres n'és una columna En l’exemple donat, la matriu A té files i columnes hom diu que A és una matriu m × n El conjunt de les matrius m ×és notat per M m X n K Una matriu pot ésser expressada també mitjançant el seu element genèric a i j , en la forma A = a i j Aquí, és l' índex de fila i j és l' índex de columna La fila formada pels elements a i…