Resultats de la cerca
Es mostren 30 resultats
functor
Matemàtiques
Morfisme entre categories
.
Un funtor F entre les categories ℒi ℛconsisteix en una regla que assigna a cada objecte A de la categoria ℒun objecte F A de la categoria ℛ, i a cada morfisme f ∈Hom X,Y , on X,Y són objectes de ℒ, li assigna un morfisme F f ∈Hom F X , F Y de tal manera que F id X =id f X i F f ₀ g = F f ₀ F
graf
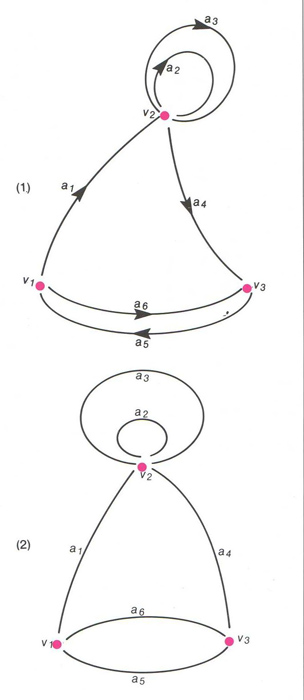
(1) Graf orientat: el camí ( a 1, a 2, a 4, a 5) és un circuit , els arcs a 2 i a 3 són bucles o rulls en el vèrtex v 2. i a 6 és un camí de v 1 a v 3. (2) graf no orientat: la cadena ( a 1, a 4, a 5) és un cicle , les arestes a 2 i a 3 són bucles o rulls en el vèrtex v 2, i a 6 és una aresta de v 1 a v 3.
© fototeca.cat
Matemàtiques
Ens constituït per un conjunt S
d’elements i per un conjunt C
de línies que uneixen els elements de S
(tot palesant una correspondència
de S
en si mateix).
Cal distingir entre un graf orientat i un graf no orientat Un graf orientat és una quaterna S, C, o, e , on S és el conjunt d’elements o vèrtexs, C és el conjunt de línies entre els vèrtexs o arcs, o és l' aplicació origen que assigna a cada arc el vèrtex del qual surt, i e és l' aplicació extrem que assigna a cada arc el vèrtex al qual arriba Un graf no orientat és una terna S, C, e , on S és el conjunt dels vèrtexs, C és el conjunt de línies entre els vèrtexs o arestes , i e és l’aplicació que assigna a cada aresta una parella de S × S , formada pels vèrtexs que uneix l’aresta en qüestió…
derivació
Matemàtiques
En un anell A, aplicació D:A→A que satisfà les següents propietats: D(a+b) = D(a)+D(b), i D(ab) = (Da)b+a(Db).
En el cos dels reals ℝ, l' aplicació derivada , que assigna a cada funció derivable f la seva derivada f´ , és una derivació
divergència
Matemàtiques
Operador diferencial.
Aquest assigna a una funció vectorial V x la quantitat escalar on V x , V y i V z són les components de V x Hom representa també div V per ∇ V
simetria
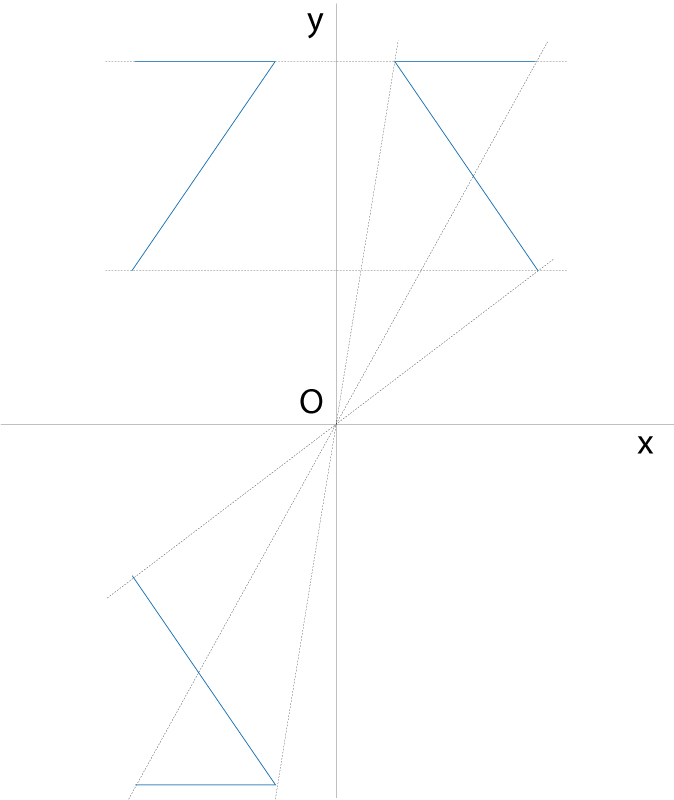
Dues figures obtingudes per simetria axial i central
© Fototeca.cat
Matemàtiques
Configuració d’un objecte que és invariant per a determinats moviments geomètrics.
Dins el concepte de simetria hom estudia modernament tots el moviments geomètrics del pla i de l’espai Una simetria axial és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a una recta donada dita eix de simetria i les distàncies de P a l’eix i de P' a l’eix són iguals Una simetria especular és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a un pla donat dit pla de simetria i les distàncies de P al pla i de P' al pla són iguals Una simetria central és una rotació de 180°…
seminorma
Matemàtiques
Aplicació d’un espai vectorial E en el conjunt de nombres reals positius.
A tot vector x de E assigna un valor ∥ x ∥ de manera que ∥ a x ∥ = | a | ∥ x ∥, i que, per a tot x, y de E , ∥ x + y ∥ ≤∥ x ∥ + ∥ y ∥ Si una seminorma compleix, a més, que ∥ x ∥=0 implica x = 0, aleshores es tracta d’una norma En ℝ 2 el pla, ∥ x , y ∥ = | x + y | és una seminorma que no és norma Tota norma és seminorma, però no inversament