Resultats de la cerca
Es mostren 3 resultats
cònica
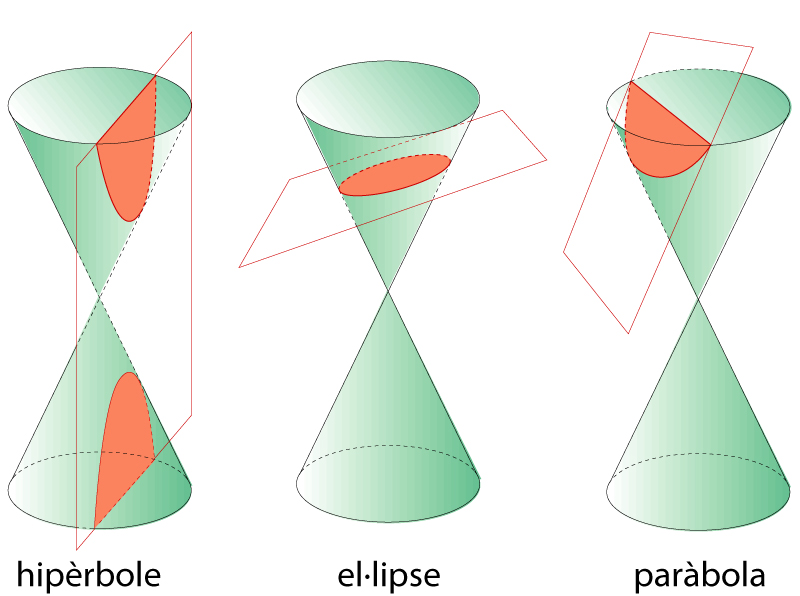
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda…
superfície desenvolupable
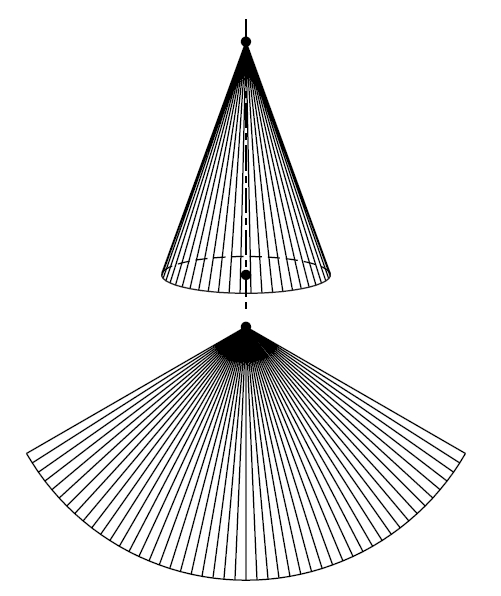
Superfície desenvolupable i el seu desenvolupament
Matemàtiques
Superfície isomètrica al pla, és a dir, que hom pot desplegar sense deformació sobre un pla.
Perquè una superfície sigui desenvolupable cal que contingui rectes superfície reglada i que el vector normal a la superfície sigui constant al llarg de cada recta En són exemples els cons, els cilindres i les superfícies constituïdes per totes les tangents a una corba en l’espai Qualsevol superfície desenvolupable és d’un d’aquests tres tipus citats