Resultats de la cerca
Es mostren 4 resultats
arrel d’una equació
Matemàtiques
Valor de la quantitat desconeguda que satisfà l’equació.
És anomenada també solució o zero de l’equació Per exemple, en l’equació el valor 1 és una arrel, car en substituir x per 1 el membre de l’esquerra s’anulla Hom empra el mot arrel, car les solucions de les equacions de grau baix, llevat de les de primer grau, es resolen comunament emprant radicals
càlcul de variacions
Matemàtiques
Estudi de la teoria dels extrems d’integrals definides tals, que llur integrant és una funció coneguda d’una o més variables independents, d’una o més variables dependents i de les seves derivades.
El problema consisteix a determinar les variables dependents, de manera que la integral sigui màxima o mínima En el cas més simple, la integral és de la forma on cal determinar la funció y x de manera que I sigui màxima o mínima També poden ésser considerades integrals de la forma on y 1 , , y n són funcions de x desconegudes o bé integrals múltiples tals com on z = z x,y és desconeguda com també poden ser-ho com integrals múltiples d’ordre superior o de diverses variables dependents L’integrant pot ésser també una funció en la qual intervinguin derivades parcials d’ordre superior En el…
mitjana
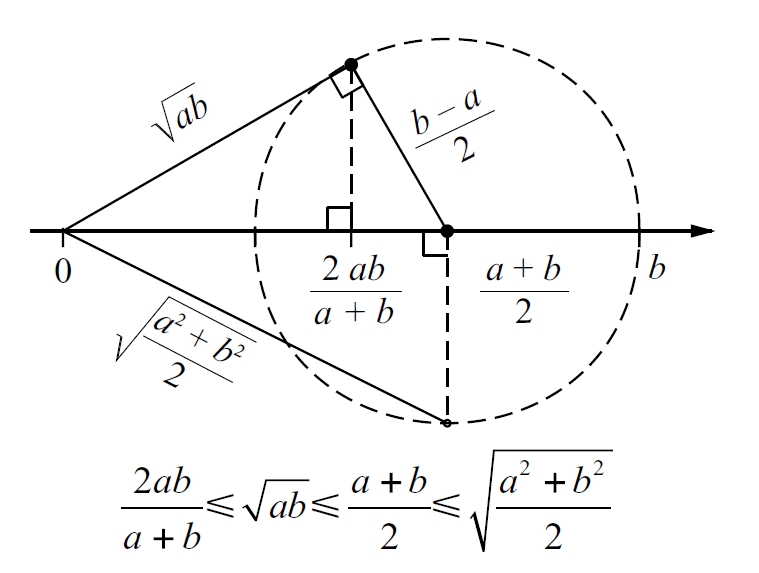
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de…
teoria de la decisió estadística
Matemàtiques
Teoria matemàtica consistent en una aproximació unificadora a l’estadística matemàtica, basada en el concepte de joc d’estratègia, introduït per John von Neumann el 1928, que inclou l’estimació puntual i per intervals, com també la teoria dels contrasts d’hipòtesis.
La inicià el treball d’Abraham Wald Statistical Decisions Functions 1949 En la teoria de la decisió hom empra mostres aleatòries per tal de prendre decisions enfront d’incerteses respecte a diverses accions, entre les quals n'hi ha que poden ésser considerades millors que les restants Per exemple, en el cas d’un contrast paramètric d’hipòtesis, hom farà servir una mostra del collectiu, n'observarà una realització i, en vista de la valor presa per la funció de decisió, acceptarà o rebutjarà la hipòtesi En la teoria de la decisió, doncs, hom considera d’una banda un sistema probabilitzat o…