Resultats de la cerca
Es mostren 25 resultats
desenvolupament en sèrie
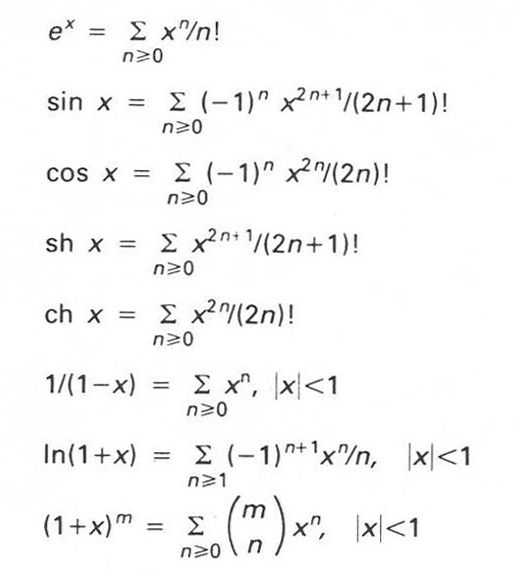
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
derivada a l’esquerra d’una funció en un punt
Matemàtiques
Donada una funció f:D ⊂ℝ→ℝi un punt a∈D, límit, si existeix, del quocient [f(a+h) - f(a)]/h, quan h tendeix a zero mantenint-se estrictament negatiu, h < 0.
Hom empra aleshores la notació f´ e a
derivada a la dreta d’una funció en un punt
Matemàtiques
Donada una funció f:D ⊂ℝ→ℝi un punt a ∈D, límit, si existeix, del quocient [f(a+h)-f(a)]/h, quan h tendeix a zero mantenint-se estrictament positiu, h>0
.
Hom empra aleshores la notació f´ d a
jacobià (d’una funció)
Matemàtiques
Determinant de la jacobiana d’una funció, quan aquesta matriu és quadrada, és a dir, quan m = n.
Hom empra la notació J = D f 1 ,, f n / D x 1 ,, x n Rep el seu nom del matemàtic Karl Jacobi
polinomis de Bernoulli
Matemàtiques
Polinomis Φn(x) definits pel desenvolupament
En termes dels nombres de Bernoulli s’expressen com Hom empra els polinomis de Bernoulli en fòrmules d' integració numèrica i en càlcul de diferències finites
extrapolació
Matemàtiques
Prolongació d’una llei o funció fora dels límits on ha estat determinada.
Hom l’empra amb dades experimentals per a arribar a la previsió d’un resultat que no pot ésser aconseguit en les condicions experimentals de treball
nombre primer de Gauss
Matemàtiques
Cadascun dels nombres primers que poden ésser expressats per la fórmula 22n + 1.
Gauss els emprà en estudiar les possibles divisions del cercle, i arribà a la conclusió que hom pot construir amb regle i compàs tot polígon regular amb un nombre primer 2 2 n + 1 de costats
Domènec Morisco i Ten
Matemàtiques
Cristianisme
Matemàtic i sacerdot.
Es doctorà en teologia a València Dirigí el Collegi de Nobles i fou secretari de la Societat Econòmica d’Amics del País de València És autor d’una Carta en que se explican las causas naturales del terremoto de 1° de noviembre de 1755 1756 i de traduccions del francès Emprà el cognom de Morico
arrel d’una equació
Matemàtiques
Valor de la quantitat desconeguda que satisfà l’equació.
És anomenada també solució o zero de l’equació Per exemple, en l’equació el valor 1 és una arrel, car en substituir x per 1 el membre de l’esquerra s’anulla Hom empra el mot arrel, car les solucions de les equacions de grau baix, llevat de les de primer grau, es resolen comunament emprant radicals
funció logarítmica
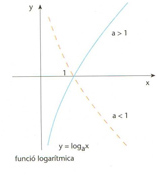
Funció logarítmica
© Fototeca.cat
Matemàtiques
Funció inversa de la funció exponencial
.
És anomenada també funció logaritme Si x = a y , on a > 0 i a ≠1, la funció logarítmica de base a fa l’assignació x → y ≡log a x Hom empra generalment la funció logarítmica de base 10 log 1 0 x i la que té per base el nombre e, o funció logaritme neperià L’extensió al cos ℂés la funció logarítmica complexa