Resultats de la cerca
Es mostren 6 resultats
polinomis de Bernoulli
Matemàtiques
Polinomis Φn(x) definits pel desenvolupament
En termes dels nombres de Bernoulli s’expressen com Hom empra els polinomis de Bernoulli en fòrmules d' integració numèrica i en càlcul de diferències finites
base
Matemàtiques
Conjunt d’elements respecte del qual s’expressen o es calculen uns altres elements.
nombres piramidals
Matemàtiques
Nombres que expressen la quantitat de boles que poden ésser disposades formant una piràmide triangular o bé quadrada.
lògica difusa
Matemàtiques
Tipus de lògica en què els valors de certesa i falsedat s’expressen en graus, i no de manera absoluta.
La lògica clàssica s’interpreta en la teoria dels conjunts cert indica la pertinença a un determinat conjunt fals, la no-pertinença La lògica difusa usa la teoria dels conjunt difusos, on la pertinença o no-pertinença és una qüestió de grau Per exemple, la pertinença al conjunt dels alts pot quedar molt clara en alguns casos, però més obscura o difusa en d’altres La lògica difusa s’usa bastant en l’anàlisi del llenguatge natural, en sistemes experts, i en general en tot tipus d’heurísticEls darrers temps s’han desenvolupat dispositius electrònics i productes comercials basats en aquest tipus…
Niels Henrik Abel

Niels Henrik Abel
© Fototeca.cat
Matemàtiques
Matemàtic noruec.
Fill d’un pastor luterà pobre, el 1817 un dels seus mestres en reconegué el talent, l’introduí en els clàssics de les matemàtiques i aconseguí el seu ingrés a la Universitat de Cristiania actualment Oslo l’any 1821, on obtingué un títol, i finançà la seva formació posterior El 1823 fou el primer en formular i resoldre una equació integral El 1824, amb l’enginyer alemany August Leopold Crelle, fundà el Journal für die reine und angewandte Mathematik ‘Revista de matemàtica pura i aplicada’, on publicà molts treballs El 1926 anà a París, aleshores centre mundial de les matemàtiques, on completà…
nombres triangulars
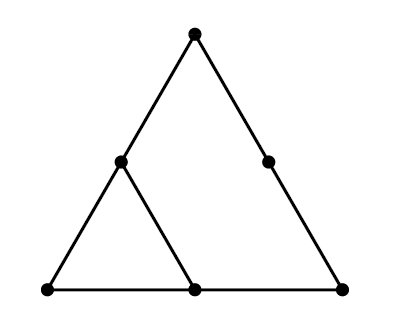
Nombres triangulars 1, 3, 6, 10 …
Matemàtiques
Nombres que són donats per la fórmula n(n+1)/2 (n essent un nombre natural qualsevol) i que expressen el nombre de boles que poden ésser disposades formant un triangle equilàter.