Resultats de la cerca
Es mostren 4 resultats
godelització
Matemàtiques
Tècnica introduïda per Kurt Gödel l’any 1931 que consisteix a reduir a nombres naturals les paraules i frases d’un cert llenguatge.
Si hom disposa d’un cert llenguatge L = { a 1 ,, a n } i a cada símbol a i li associa un cert nombre senar g a i per exemple, g a i = 2 i + 1 i, a cada paraula , on cada és una de les lletres a j ∈ L , el nombre , on p r és el r -èsim nombre primer Ara hom pot estendre aquesta tècnica a frases, on cada OOO és una de les lletres
arbre
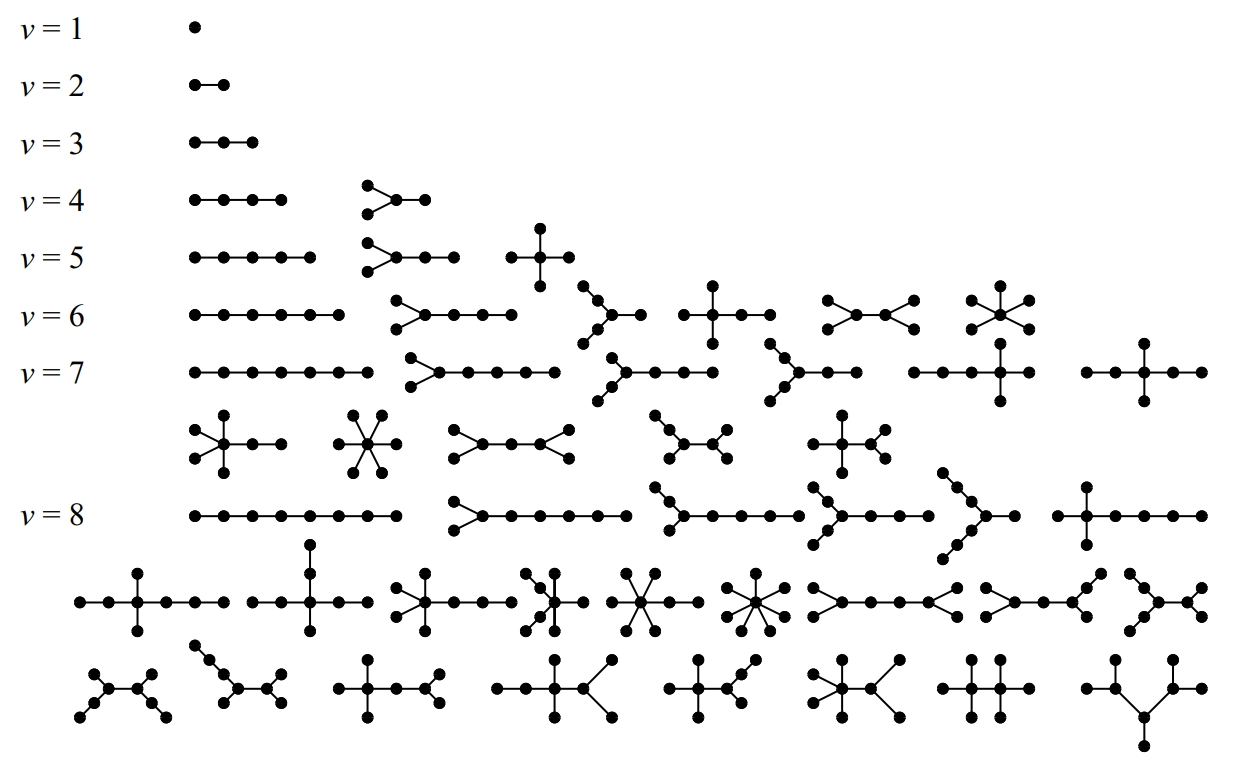
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la modelització de…
teoria de la computació
Matemàtiques
Branca de les matemàtiques que estudia problemes de decidibilitat.
Com és usual en la història de les matemàtiques, té orígens aparentment molt diferents que finalment conflueixen i permeten d’establir el que esdevé una teoria enormement potent i irrenunciable Cal remarcar-ne el problema diofàntic plantejat per David Hilbert l’any 1900, i el problema de les paraules que sorgí en el món de la topologia algèbrica Es tracta de dos problemes típics de decidibilitat és a dir, aquells en què cal disposar d’un mètode que permeti de decidir una o altra de dues opcions atesa una equació diofàntica, té solució, són equivalents dues paraules donades per…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres…