Resultats de la cerca
Es mostren 2 resultats
autòmat finit indeterminista
autòmat finit indeterminista
Matemàtiques
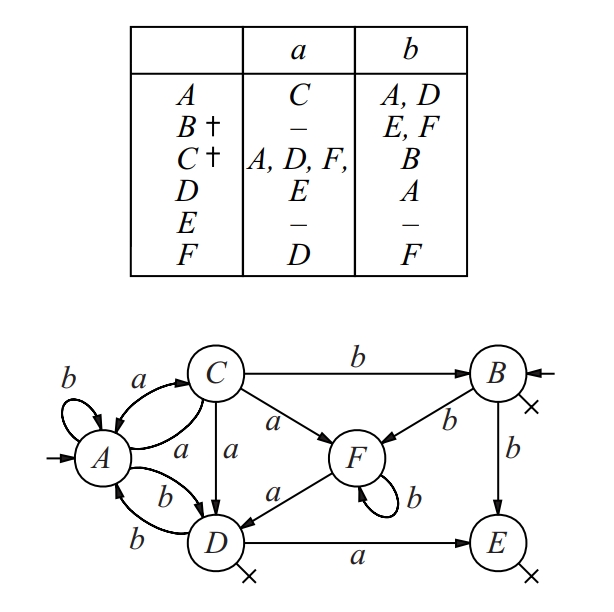
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
Lotfi A. Zadeh
Lofti A. Zadeh
© Franklin Institute Awards
Matemàtiques
Matemàtic nord-americà d’origen azerbaidjanès.
Estudià a Teheran enginyeria elèctrica El 1944 s’installà als EUA i estudià al Massachusetts Institute of Technology i a la Columbia University, on es doctorà el 1949 Fou professor d’aquesta universitat i, posteriorment, de la University of California, on dirigí el Berkeley Initiative for Soft Computing Feu notables contribucions a la teoria dels sistemes, exposades en l’obra Linear System Theory 1963, amb CA Desoer El 1964 introduí el mètode anomenat dels conjunts difusos , per tal de tractar d’una manera matematicooperativa la vaguetat associada a la parla habitual, teoria que aplicà als…