Resultats de la cerca
Es mostren 6 resultats
digraf de Kautz
digraf de Kautz
Fototeca.cat
Matemàtiques
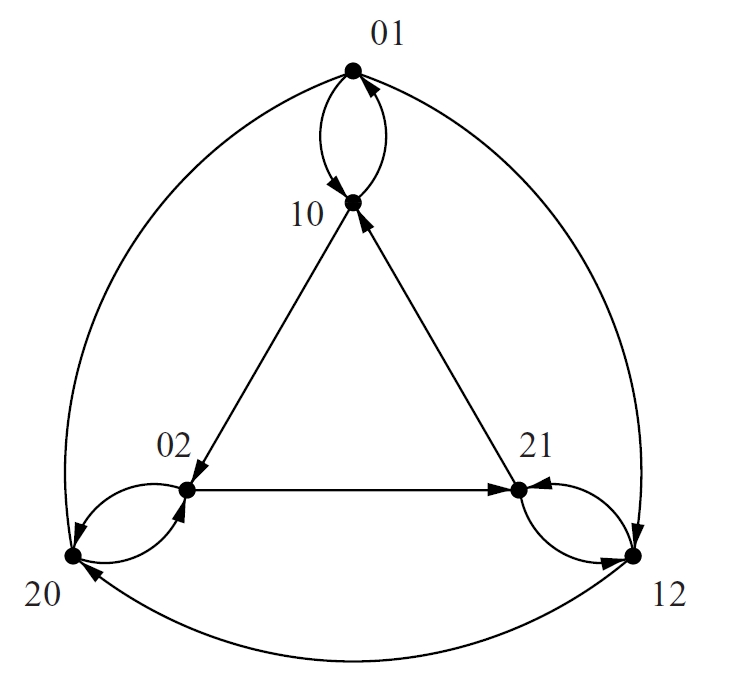
Digraf K(d, D) que té per conjunt de vèrtexs el de totes les paraules de longitud D que es poden formar amb els d + 1 símbols diferents d’un alfabet, de manera que dos símbols consecutius sempre siguin diferents.
Una paraula és adjacent respecte a una altra si la primera sense el símbol inicial és igual a la segona sense el símbol final El digraf de Kautz K d , D té diàmetre D
Bertrand François Barrême
Matemàtiques
Aritmètic francès.
Autor del primer curs d’aritmètica comercial a França Els seus llibres Comptes faits du grand commerce 1670 i Livre nécessaire pour tous les comptables 1677 tingueren molta difusió El seu cognom ha originat la paraula barem
godelització
Matemàtiques
Tècnica introduïda per Kurt Gödel l’any 1931 que consisteix a reduir a nombres naturals les paraules i frases d’un cert llenguatge.
Si hom disposa d’un cert llenguatge L = { a 1 ,, a n } i a cada símbol a i li associa un cert nombre senar g a i per exemple, g a i = 2 i + 1 i, a cada paraula , on cada és una de les lletres a j ∈ L , el nombre , on p r és el r -èsim nombre primer Ara hom pot estendre aquesta tècnica a frases, on cada OOO és una de les lletres
digraf de De Brujin
digraf de De Brujin
Matemàtiques
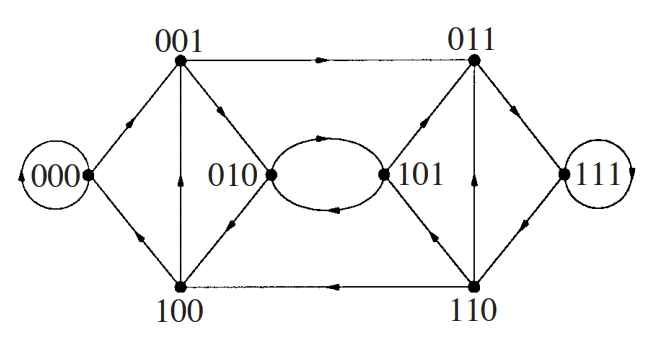
Digraf B(d,D) que té per conjunt de vèrtexs totes les paraules de longitud D que es poden formar amb els d símbols diferents d’un alfabet i tal que una paraula és adjacent respecte a una altra si la primera sense el símbol inicial és igual a la segona sense el símbol final.
El digraf de De Bruijn és un digraf eulerià, d -regular, que té d elevat a D + 1 arcs Els digrafs de De Bruijn són útils en el disseny de grans xarxes d’interconnexió
autòmat finit determinista
autòmat finit determinista
Matemàtiques
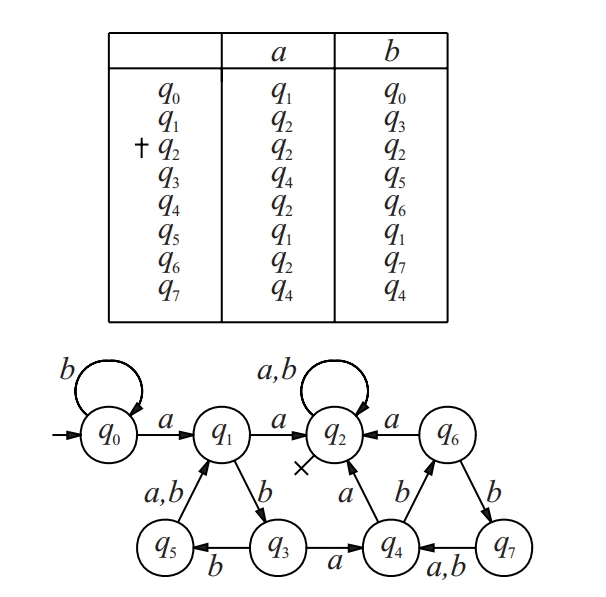
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
Aristòtil

Còpia romana d’Aristòtil del període imperial (segle I o II dC) d’un bronze perdut realitzat per Lísip (Museu del Louvre)
Yuxuan Wang (CC BY-NC-ND 2.0)
Filosofia
Matemàtiques
Filòsof i científic grec, un dels esperits més potents i influents de la història.
Vida i obra Del clan dels asclepíades, era fill de Nicòmac, metge i amic d’Amintes II de Macedònia A divuit anys ingressà a l’Acadèmia Els primers temps fou el deixeble predilecte de Plató, però les divergències posteriors els distanciaren A la mort del mestre 347, Aristòtil abandonà Atenes i passà tres anys a Assos, on s’uní amb Herpillis, de la qual tingué un fill, Nicòmac, al qual dedicà un dels tractats d’ètica D’Assos passà a Mitilene d’aquesta època daten molts dels seus treballs de biologia En 343-342 aC Filip de Macedònia li encarregà l’educació d’Alexandre Aristòtil, que atribuïa una…