Resultats de la cerca
Es mostren 8 resultats
problema de les paraules
Matemàtiques
Problema d'àlgebra.
D’una banda si hom disposa d’un alfabet finit OOO = {a 1 ,,a n } i, per concatenació, construeix els mots M = ζ 1 ζ r , on cada símbol ζ i és una de les lletres a j ∈ OOO d’aquest alfabet i r ∈ ℕ si, d’altra banda, hom disposa d’un cert diccionari que estableix l’equivalència de certes parelles de mots i, finalment, hom accepta el fet que, en substituir en un mot M = M 1 mM 2 un cert sumbmot m per un altre mot m´ equivalent, obté un mot equivalent M´ = M 1 m' M 2 Cal plantejar la pregunta següent donats dos mots arbitraris M i N , hi ha algun algorisme que permeti de decidir si són…
teoria de la computació
Matemàtiques
Branca de les matemàtiques que estudia problemes de decidibilitat.
Com és usual en la història de les matemàtiques, té orígens aparentment molt diferents que finalment conflueixen i permeten d’establir el que esdevé una teoria enormement potent i irrenunciable Cal remarcar-ne el problema diofàntic plantejat per David Hilbert l’any 1900, i el problema de les paraules que sorgí en el món de la topologia algèbrica Es tracta de dos problemes típics de decidibilitat és a dir, aquells en què cal disposar d’un mètode que permeti de decidir una o altra de dues opcions atesa una equació diofàntica, té solució, són equivalents dues paraules donades per endavant L’any…
godelització
Matemàtiques
Tècnica introduïda per Kurt Gödel l’any 1931 que consisteix a reduir a nombres naturals les paraules i frases d’un cert llenguatge.
Si hom disposa d’un cert llenguatge L = { a 1 ,, a n } i a cada símbol a i li associa un cert nombre senar g a i per exemple, g a i = 2 i + 1 i, a cada paraula , on cada és una de les lletres a j ∈ L , el nombre , on p r és el r -èsim nombre primer Ara hom pot estendre aquesta tècnica a frases, on cada OOO és una de les lletres
àlgebra

Triàngle numèric, més tard conegut com a triangle de Pascal, d’un manuscrit xinès del 1303
© Fototeca.cat
Matemàtiques
Branca de les matemàtiques que estudia les estructures algèbriques dels conjunts.
Hom l’aplica, per tant, en les situacions on hi ha un conjunt ben definit i una noció clara d’operació entre els seus elements operació interna o entre aquests i els elements d’altres conjunts operació externa L’àlgebra ha evolucionat des de l’interès inicial per a resoldre problemes fonamentalment pràctics fins al desenvolupament del mètode abstracte Dues inclinacions diferents han desembocat en l’àlgebra moderna D’una banda, l’ àlgebra clàssica , simple instrument per a fer càlculs i resoldre equacions que usava només els conceptes immediats que hom reconeixia al…
digraf de Kautz
digraf de Kautz
Fototeca.cat
Matemàtiques
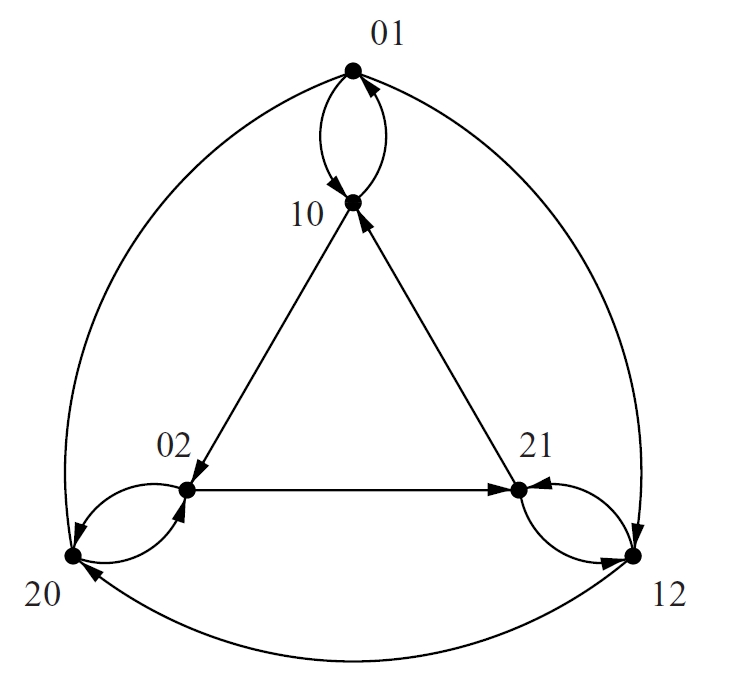
Digraf K(d, D) que té per conjunt de vèrtexs el de totes les paraules de longitud D que es poden formar amb els d + 1 símbols diferents d’un alfabet, de manera que dos símbols consecutius sempre siguin diferents.
Una paraula és adjacent respecte a una altra si la primera sense el símbol inicial és igual a la segona sense el símbol final El digraf de Kautz K d , D té diàmetre D
digraf de De Brujin
digraf de De Brujin
Matemàtiques
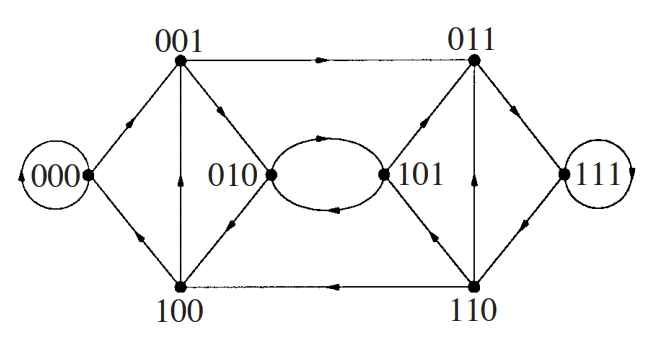
Digraf B(d,D) que té per conjunt de vèrtexs totes les paraules de longitud D que es poden formar amb els d símbols diferents d’un alfabet i tal que una paraula és adjacent respecte a una altra si la primera sense el símbol inicial és igual a la segona sense el símbol final.
El digraf de De Bruijn és un digraf eulerià, d -regular, que té d elevat a D + 1 arcs Els digrafs de De Bruijn són útils en el disseny de grans xarxes d’interconnexió
autòmat finit determinista
autòmat finit determinista
Matemàtiques
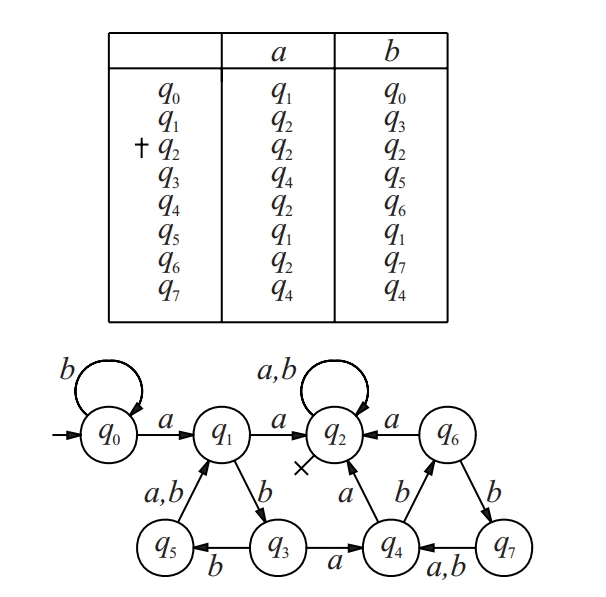
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
autòmat finit indeterminista
autòmat finit indeterminista
Matemàtiques
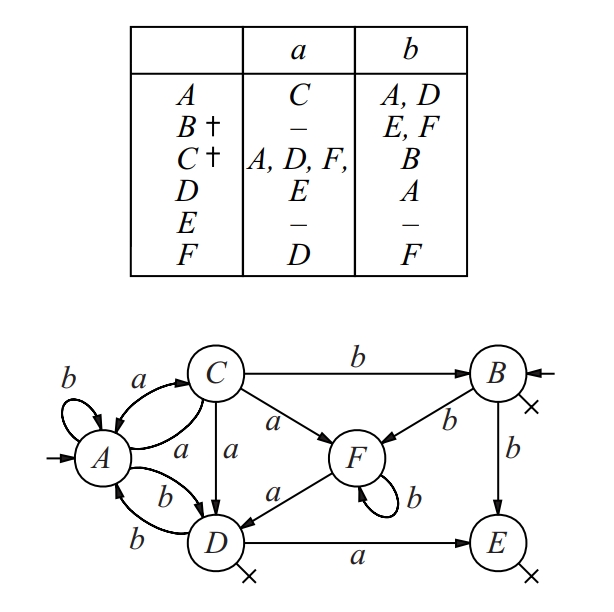
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció