Resultats de la cerca
Es mostren 5 resultats
Henri Léon Lebesgue
Matemàtiques
Matemàtic francès.
Creador de la integral que duu el seu nom i autor de Leçons sur l’intégration et la recherche des fonctions primitives 1904, obrí noves perspectives en la teoria de funcions
funció primitiva d’una funció
Matemàtiques
Donada una funció f(x), funció F(x) tal que F´(x)=f(x) (on F´(x) és la derivada de la funció F(x)).
Hom diu aleshores que F x és la funció primitiva o, simplement, la primitiva, de f x Les primitives d’una funció són obtingudes mitjançant la determinació de la integral indefinida d’aquesta, F x =∫ x a f t
integral indefinida
Integrals indefinides de les funcions usuals
©
Matemàtiques
Donada una funció f:(a,b] ⊂ℝ→ℝ, funció F definida en [a,b] per la integral (definida) F(x)= ∫fxsup;a&(t)dt.
Aquesta funció és una funció primitiva de la funció f , per tal com la seva derivada és igual a f , F' x = f x , i, de fet, genera la resta de funcions primitives de f , G x = F x + C , essent C una constant
nombre natural
Matemàtiques
Nombre que serveix per a comptar els elements d’un conjunt.
La manera més freqüent de representar els nombres naturals és el sistema de numeració decimal, i el conjunt dels nombres naturals acostuma a ésser representat amb la lletra ℕ En la concepció dels nombres naturals, i també de les altres menes de nombres, hom pot donar prioritat a l’aspecte intuïtiu o a l’aspecte lògic Des del punt de vista intuïtiu, un nombre natural és una qualitat dels conjunts equipotents així, la classe de tots els conjunts equipotents amb el conjunt { X o Δ} és el nombre tres L’operació “unió de conjunts sense elements comuns” engendra l’operació de “sumar nombres…
integral
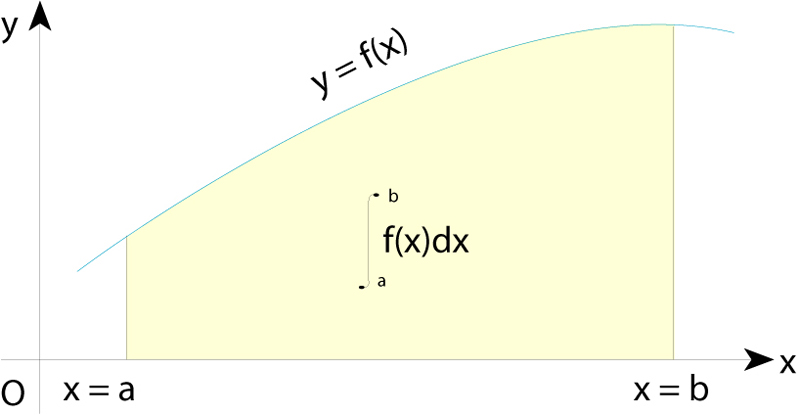
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b ,…