Resultats de la cerca
Es mostren 91 resultats
angles corresponents

Angles determinats per una secant a dues rectes: alterns, corresponents, oposats pel vèrtex i conjugats
Matemàtiques
Els dos angles de cada una de les quatre parelles formades per dues rectes tallades per una secant, ambdós a un mateix costat de la secant, un d’ells intern i l’altre extern i no adjacents.
Si les dues rectes són paralleles, dos angles corresponents són iguals
angles alterns
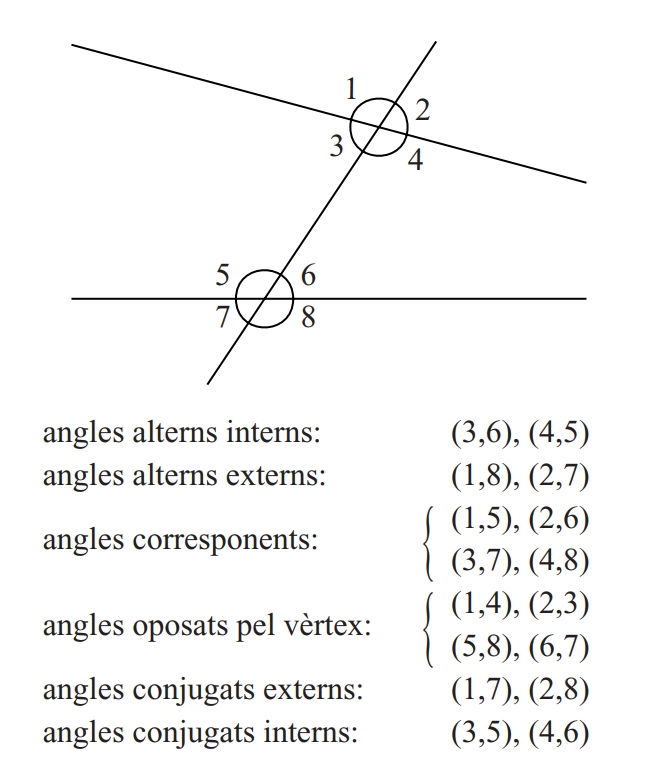
Angles determinats per una secant a dues rectes: alterns, corresponents, oposats pel vèrtex i conjugats
Matemàtiques
Els dos angles de cada una de les quatre parelles formades per dues rectes tallades per una secant, cada un d’ells a un costat diferent de la secant, ambdós externs (alterns externs) o interns (alterns interns) i no adjacents.
Si les dues rectes són paralleles, dos angles alterns són iguals
bisectriu
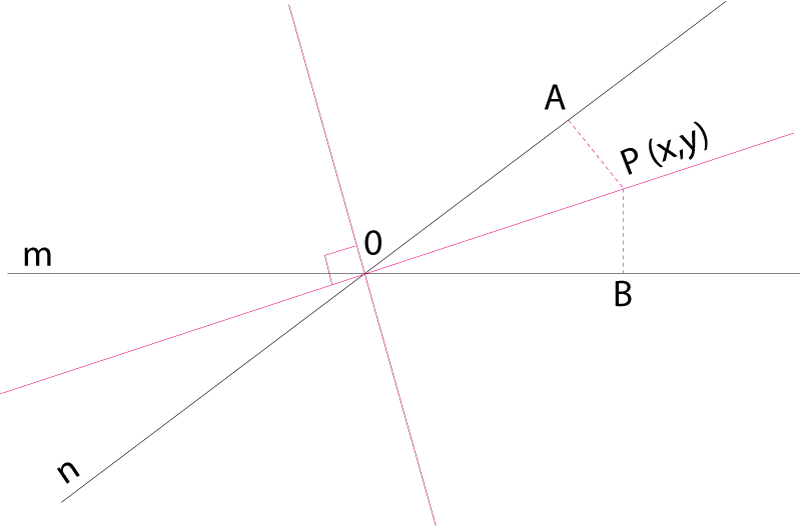
Bisectrius corresponents als quatre angles determinats per dues rectes que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels costats d’un angle, el qual divideix, per tant, en dos angles iguals.
Dues rectes que es tallen determinen quatre angles, iguals dos a dos Llurs bisectrius són dues rectes perpendiculars entre elles En considerar un dels quatre angles hom distingeix la bisectriu interior i la bisectriu exterior Les equacions de les bisectrius dels angles que determinen dues rectes que es tallen, les d’equacions de les quals són, en una referència cartesiana normal, A 1 x + B 1 y + C 1 = 0 i A 2 x + B 2 y + C 2 =0, són
teorema de Tales
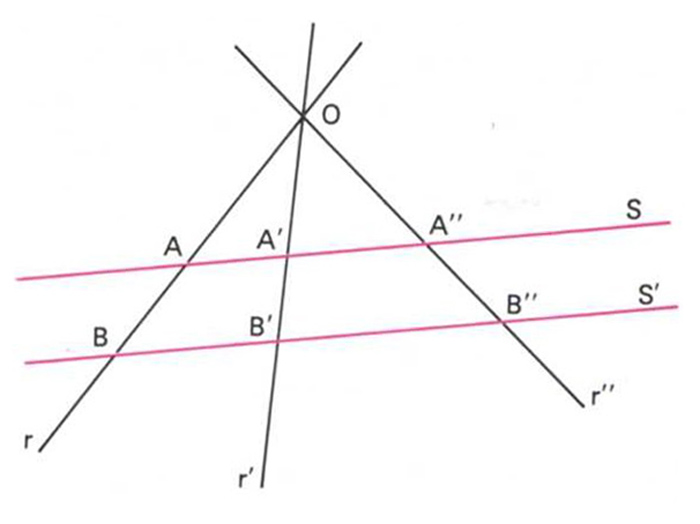
Teorema de Tales
© fototeca.cat
Matemàtiques
Teorema que estableix la proporcionalitat dels segments interceptats per rectes paral·leles sobre un feix de rectes concurrents.
Així, si tres rectes r, r´ i r’ que es tallen en O, són interceptades per les rectes paralleles en S, i en els punts B, B´ i B’ en S´, el teorema de Tales permet d’establir, entre d’altres, les següents relacions
paral·lel | paral·lela
Matemàtiques
Dit de les rectes que tenen la mateixa direcció.
En el pla, si dues rectes no es tallen són paralleles
superfície reglada
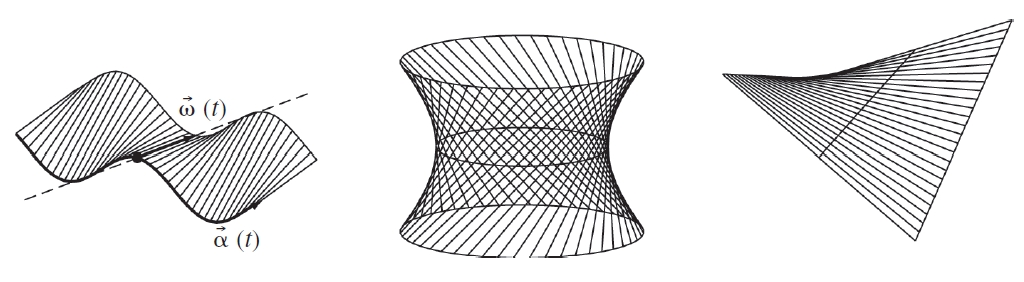
Superfícies reglades
Matemàtiques
Superfície engendrada per una família infinita de rectes que depenen d’un paràmetre.
Cadascuna d’aquestes rectes és anomenada generatriu de la superfície els procediments habituals per a definir-les són donar les equacions d’una recta en l’espai amb un paràmetre variable, o bé donar tres corbes directrius i prendre com a generatrius les rectes que recolzen sobre aquestes tres corbes Hi ha dues classes de superfícies reglades si en tots els punts d’una mateixa generatriu la superfície té el mateix pla tangent, es tracta d’una superfície desenvolupable , i la superfície pot ésser construïda cargolant oportunament un o diversos trossos de paper però si…
superfície cilíndrica
Matemàtiques
Superfície engendrada per una família de rectes paral·leles entre elles que recolzen sobre una corba donada, plana o no, anomenada directriu de la superfície
.
El cas més simple superfície circular cilíndrica es presenta quan la corba directriu és una circumferència i les rectes generatrius són perpendiculars al pla de la circumferència
pla tangent
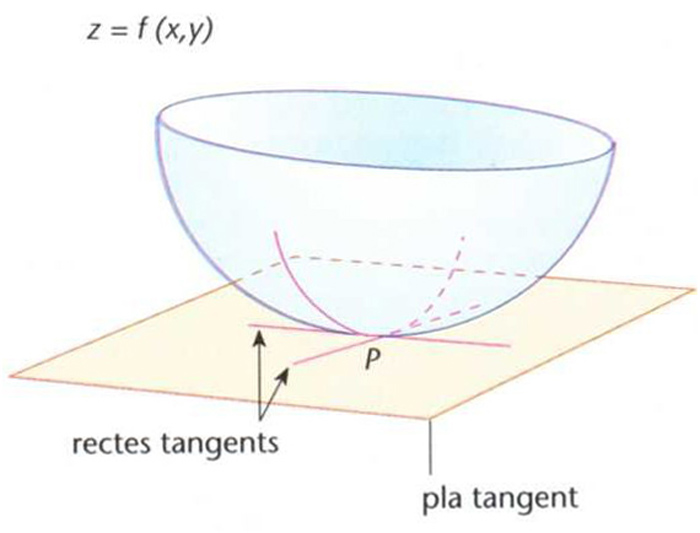
Pla tangent i dues rectes tangents a la superfície z= f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Donada una superfície z=f(x,y) i un punt P [x0, y0f(x0, y0)], pla que conté les rectes tangents en aquest punt a totes les corbes contingudes en la superfície considerada i que passen pel punt [x0, y0, f(x0, y0)].
L’equació d’aquest pla és
teorema de Desargues
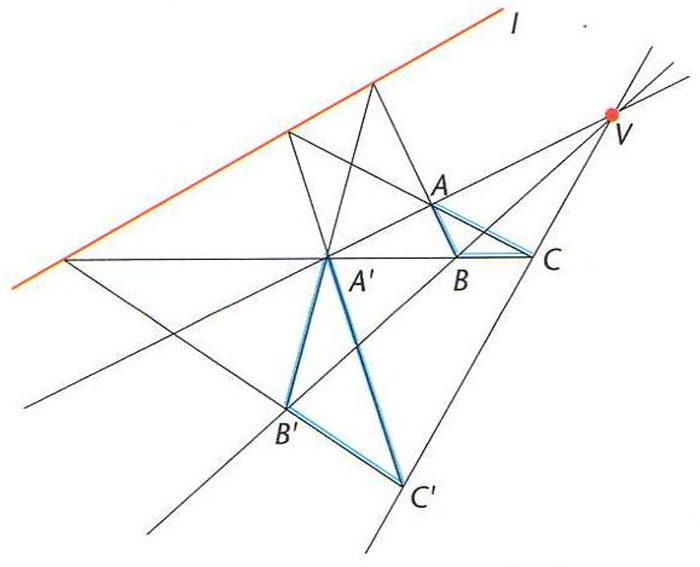
V és el punt de concurrència de les rectes AA’, BB' i CC' i l és la línia que conté els punts de concurrència de AB i A'B', de BC i B'C' i de CA i C'A'
© fototeca.cat
Matemàtiques
Teorema segons el qual, donats dos triangles ABC i A’B’C’ tals que les rectes AA’, BB’ i CC’ són concurrents, els punts de concurrència de AB i A’B’, de BC i B’C’ i de CA i C’A’ són alineats.
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina