Resultats de la cerca
Es mostren 16 resultats
punt interior
Matemàtiques
En un conjunt A d’un espai topològic, punt del qual existeix un entorn totalment inclòs en A
.
El conjunt de tots els punts interiors de A és anomenat interior de A i hom el designa per Å
pla

Equació del pla
© fototeca.cat
Matemàtiques
Superfície tal que qualsevol recta que passi per dos dels seus punts es troba totalment continguda en la dita superfície.
Els plans, juntament amb els punts i les rectes, són els elements geomètrics primitius en l’axiomatització de Hilbert de la geometria D’altra banda, un pla és determinat per tres punts no alineats, o bé per dues rectes que es tallin o siguin paralleles, o bé per un punt i una recta que no contingui el punt A l’espai euclidià ℝ 3 un pla pot ésser representat per l’equació A x— x 1 + B y— y 1 + C z— z 1 = 0, en la qual x 1 , y 1 , z 1 són les tres coordenades d’un punt P 1 donat del pla, A, B, C són les tres components d’un vector N normal al pla, i x, y, z són les tres coordenades d’un…
conjunt ordenat
Matemàtiques
Conjunt X
proveït d’una relació d’ordre ≤.
Si la relació d’ordre és parcial, el conjunt OOO X ,≤OOO és parcialment ordenat i, si és total, és totalment ordenat Una relació d’ordre és parcial si compleix les propietats reflexiva x ≤ x , transitiva si x ≤ y i y ≤ z , aleshores x ≤ z i antisimètrica si x ≤ y i y ≤ x , aleshores x = y I és total quan és parcial i, a més, tota parella d’elements és comparable qualssevol que siguin x , y , x ≤ y o y ≤ x
convex | convexa
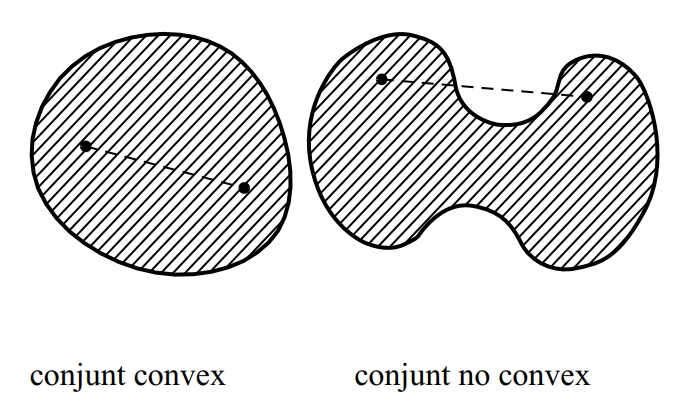
convex
Matemàtiques
Dit de la figura tal que el segment que uneix un parell qualsevol dels seus punts està totalment contingut en el seu interior.
dens | densa
Matemàtiques
Dit d’un conjunt C totalment ordenat tal que entre dos elements qualssevol, a i b ∈C, hi ha un tercer element c.
Els conjunts dels nombres racionals ℚi dels reals ℝsón densos
notació
Matemàtiques
Conjunt de símbols utilitzat per a representar els ens i les operacions matemàtiques.
En teoria, l’elecció de la notació és totalment arbitrària Ara bé, la resolució dels problemes matemàtics i especialment els de matemàtica moderna és molt més simple si hom utilitza una notació adient En aquest aspecte, cal recordar només el progrés que per als càlculs aritmètics representà la substitució de la notació romana o sistema de numeració romana pel sistema de numeració decimal actual, el qual utilitza l’anomenada notació posicional o de posició , que consisteix en el fet que el valor de cada símbol no és determinat només per la seva forma sinó també per la posició que…
Alexander Grothendieck

Alexander Grothendieck
Matemàtiques
Matemàtic francès d’origen alemany.
Fill d’un anarquista jueu d’origen rus i d’una escriptora restà orfe de pare després que els nazis l’haguessin internat a Auschwitz Visqué amb la seva mare a França, i estudià matemàtiques a Montpeller i a París Després d’ensenyar al Brasil i als Estats Units, el 1958 s’incorporà a l’Institut des Hautes Études Scientifiques IHES, on desenvolupà la carrera acadèmica Considerat un dels primers matemàtics del segle XX, efectuà aportacions fonamentals a diversos camps de la matemàtica, primer en l’ anàlisi funcional teoria dels espais nuclears i després en la seva obra monumental i inacabada,…
Carl Friedrich Gauss
Carl Friedrich Gauss
Matemàtiques
Matemàtic alemany.
De família humil, extraordinàriament dotat per a les matemàtiques, pogué rebre ensenyament superior gràcies a la protecció del duc de Brunsvic, que l’envià a la Universitat de Göttingen Director de l’observatori i professor d’astronomia en aquella ciutat, hi residí fins a la mort, dedicat totalment a una fecunda tasca intellectual Els matemàtics li deuen aportacions transcendentals en la teoria dels nombres i en l’àlgebra noció de congruència i notació corresponent, sistematització de l’ús de demostració rigorosa del teorema fonamental de l’àlgebra, teoria de determinants , etc,…
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta…