Resultats de la cerca
Es mostren 22 resultats
funció tangent
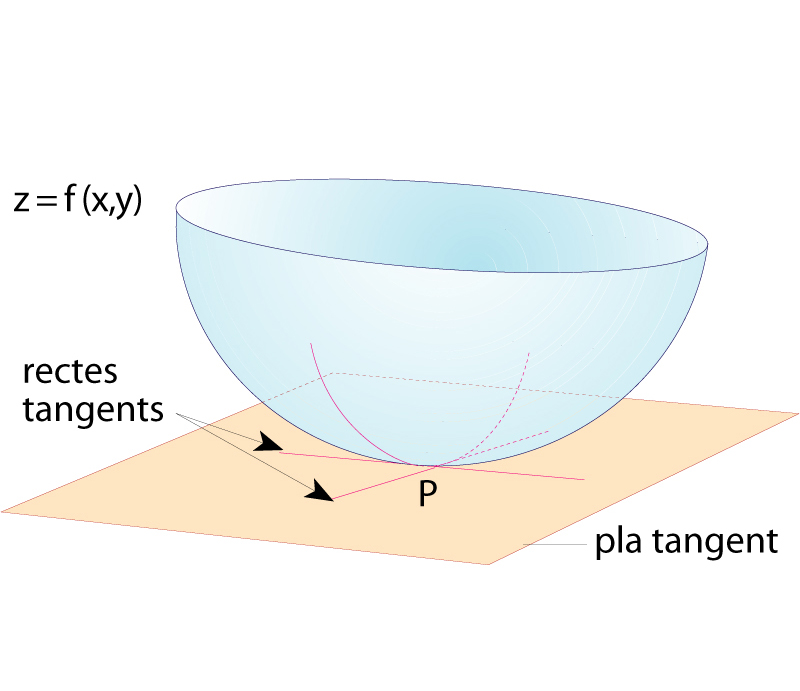
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
funció tangent complexa
Matemàtiques
Funció tg: ℂ-{(k+1/2)π, k ∈ℤ} →ℂ, definida per l’assignació z →tgz = (sinz)/(cosz), on sin z és la funció sinus complex i cos z la funció cosinus complex.
Hom pot comprovar que tg z = e 2 i z - 1 / i e 2 i z + 1
analogies
Matemàtiques
Fórmules de resolució de triangles esfèrics, emprades generalment per a comprovar els resultats trobats per altres mètodes (grups de Bessel, etc.).
Hom distingeix les fórmules trobades per Neper 1614 que donen el valor de tg 1 / 2 A + B, tg 1 / 2 a + b, tgs41/ 2 A - B, tg 1 / 2 a - b i les de Delambre i Gauss 1808, que relacionen els angles d’un triangle esfèric amb els costats oposats
funció tangent hiperbòlica complexa
Matemàtiques
Funció th: ℂ-{i(k+1/2)π, k ∈ℤ} →ℂdefinida per l’assignació z →th z=(sh z/(ch z), on sh x i ch z són les funcions sinus i cosinus hiperbòlics complexos, respectivament.
Se satisfà que th z = e z - e - z / e z + e - z , i que th z =- i tgiz, i que th iz = i tg z , on tg és la funció tangent complexa
ch
Escriptura i paleografia
Dígraf català antic que representava el so velar sord [k] i que a vegades hom emprava en posició medial (archebisbe, eucharistia) i inicial (chor, Christ) en l’escriptura de mots d’origen grec i, especialment i d’una manera general, en posició final (bosch, amich) (h).
En la codificació ortogràfica moderna ha estat simplificat en c Dialectalment o incorrectament hom l’ha emprat també per a representar els sons palatals x ix i j g , tx i tj tg En català modern roman únicament en l’escriptura d’alguns cognoms
angle de polarització
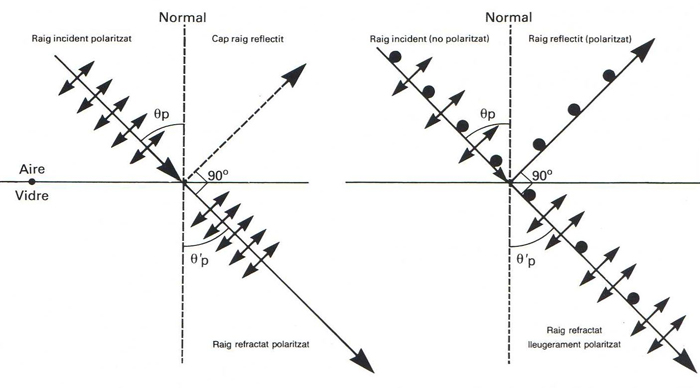
A la figura de l’esquerra, la llum incident només té component paral·lela al pla d’incidència (fletxes), de manera que quan l’angle d’incidència és igual a l’angle de polarització, O subp , no hi ha llum reflectida; a la figura de la dreta, la llum incident té component paral·lela (fletxes) i component perpendicular (punts) al pla d’incidència, de manera que quan l’angle d’incidència és igual a l’angle de polarització, O subp , la llum reflectida no és nul·la, ja que conté la component perpendicular (punts) al pla d’incidència
© fototeca.cat
Física
Angle amb què ha d’incidir un raig de llum sobre una superfície separadora de dos medis d’índexs de refracció n
i n´
per tal que en la llum reflectida no hi hagi component paral·lela al pla d’incidència.
Segons les fórmules de Fresnel, l’angle de polarització φ π satisfà φ π + φ´ p = 90°, essent φ´ p el corresponent angle de refracció D’acord amb la llei de la refracció resulta que tg φ π = n´/n llei de Brewster, fórmula que dóna el valor de φ π , i que el raig reflectit i el refractat són perpendiculars entre ells
fórmula de Breit-Wigner
Física
Fórmula que expressa la secció eficaç de la captura radiativa d’una partícula A (p ex, un neutró) per un nucli B, quan l’energia E de la partícula incident A és molt propera a un nivell excitat.
energia de ressonància E 0 del nucli compost A + B σ E = c E — E 0 2 + γ 2 /4 - 1 , essent c una constant que depèn de les característiques de la collisió i γ l’amplada total del nivell excitat E 0 , la qual és relacionada amb la vida mitjana τ d’aquest nivell pel principi d'incertesa tg = ħ
funció exponencial complexa
Matemàtiques
Funció f:ℂ→ℂque resulat d’estendre a ℂla funció exponencial.
És anomenada també, simplement, exponencial complexa És definida per l’assignació on z ∈ℂ És periòdica de període 2π i És relacionada amb les funcions trigonomètriques sinus i cosinus per la relació e x + i y = e x cos y + sin y , que permet excriure la forma exponencial d’un nombre complex, z = x + iy = ρ e i ϑ on és el mòdul de z i ϑ = arc tg y/x n'és l’argument
tangent d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i una circumferència de radi unitat centrada en el punt d’intersecció dels eixos (cercle goniomètric), i un segment que forma un angle α amb l’eix d’abcisses x, longitud del segment, perpendicular a l’eix d’abcisses, deteminat entre el punt de la circumferència de coordenades (1,0) i el punt en què aquest segment s’interseca amb el segment inclinat l’angle α en qüestió.
Aquesta longitud és la tangent de l’angle α, i és denotada per tgα És vàlida la següent igualtat tgα=sin α/cos α, on sin és el sinus d’un angle i cos és el cosinus d’un angle La tangent de l’angle α determinat entre dos segments qualssevol és la tangent de l’angle que, dibuixat sobre el cercle goniomètric, té la mateixa obertura que α Algunes fòrmules trigonomètriques relatives a la tangent d’un angle són tgα+β=tgα+tgβ/1-tgα- tgβ tg-α=-tgα tgα+tgβ- =sinα+β/cosα cosβ