Resultats de la cerca
Es mostren 80 resultats
Càlcul de variacions, equacions diferencials, mecànica, equacions, nombres (Lagrange)
Càlcul de variacions, equacions diferencials, mecànica, equacions, nombres Lagrange
lagrangià
Tecnologia
Funció L = T-V, on T és l’energia cinètica i V és l’energia potencial d’un sistema.
mecànica analítica
Tecnologia
Part de la mecànica racional que comença amb la magistral obra de Joseph-Louis Lagrange Mécanique analytique (1788) i continua amb les obres de W.R.Hamilton (1834) i C.G.Jacobi (1842).
Gràcies al progrés que havia experimentat l’anàlisi infinitesimal, Lagrange reduí al mínim els postulats de la dinàmica i en deduí, per mitjà del càlcul diferencial i del càlcul integral, unes fórmules generals, anomenades equacions de Lagrange, aplicables a tota mena de problemes mecànics concrets, en les quals l’energia cinètica té un paper principal Encara actualment les equacions de Lagrange són aplicades correntment, sobretot als sistemes de sòlids, com ara als d’oscilladors mecànics o elèctrics, i també als de corpuscles microfísics WRHamilton…
grup Troià
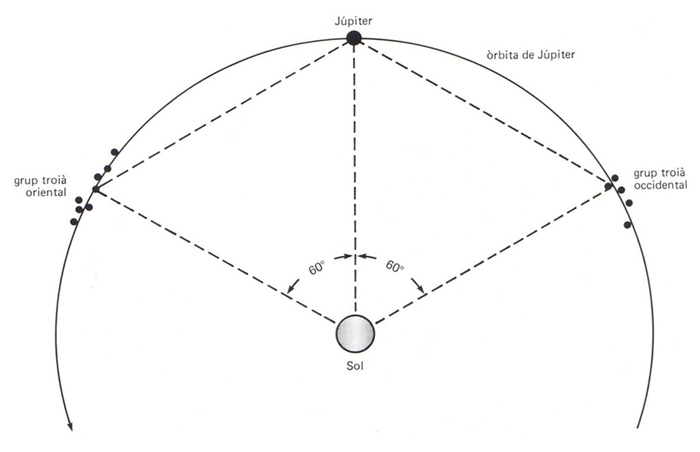
Grup Troià
© fototeca.cat
Astronomia
Conjunt d’asteroides que tenen òrbites semblants a la de Júpiter, i les posicions dels quals relatives a aquest darrer no varien amb el temps.
Els asteroides d’aquest grup són situats entorn de dos punts l’un precedeix Júpiter en el seu moviment, i l’altre el segueix Aquests dos punts, units amb Júpiter i el Sol, formen dos triangles que tenen un costat comú, que és la recta que uneix Júpiter amb el Sol L’existència d’aquests punts d’equilibri fou predita per Lagrange en estudiar un cas particular del problema de tres cossos el cas en què un dels cossos té una massa negligible en comparació de la massa dels altres dos punts de Lagrange El primer asteroide d’aquest grup fou descobert l’any 1906 per Max Wolf l’any 1949 hom ja en…
principi de D’Alembert
Física
Principi diferencial de la mecànica que permet, mitjançant l’addició de les forces d’inèrcia i les forces aplicades a un sistema, derivar les equacions del moviment d’un sistema no sotmès a forces de fricció i tal que el treball virtual de les forces de lligam s’anul·li.
De l’expressió inicial s’obtenen, en canviar a coordenades generalitzades d’un sistema conservatiu amb lligams holònoms, les equacions de Lagrange
Alfred Serret
Matemàtiques
Matemàtic francès.
Estudià la teoria de funcions, els grups i les equacions diferencials Publicà diverses obres, com Traité d’arithmétique 1852, Traité de trigonométrie 1850 i també les obres de Lagrange 1867-77
Manel Escrig
Esquí
Esquiador nàutic.
Vinculat al Club Nàutic d’Arenys de Mar, fou campió d’Espanya d’esquí nàutic 1975, 1976 Amb l’Escuderia Lagrange-Escrig assolí el tercer lloc al Campionat d’Espanya offshore 1983
principi de Hamilton
Física
Una de les formes d’enunciar el principi de la mínima acció.
L' acció elemental és definida a partir del lagrangià, dA = L dt , i el principi afirma que el moviment del sistema entre dos instants t 1 i t 2 és tal que l’acció és un extremal, és a dir, un màxim o un mínim Hom en dedueix les equacions de Lagrange
Alexandre Vandermonde
Matemàtiques
Matemàtic francès.
Estudià les equacions cúbiques i quadràtiques i d’altres, com la del tipus x n -1 = 0 per a tot n nombre primer Amb Lagrange elaborà mètodes per a resoldre equacions 1771, i són especialment importants els estudis sobre els determinants 1772 S'ocupà també de la mecànica i de l’acer