Resultats de la cerca
Es mostren 515 resultats
pla tangent
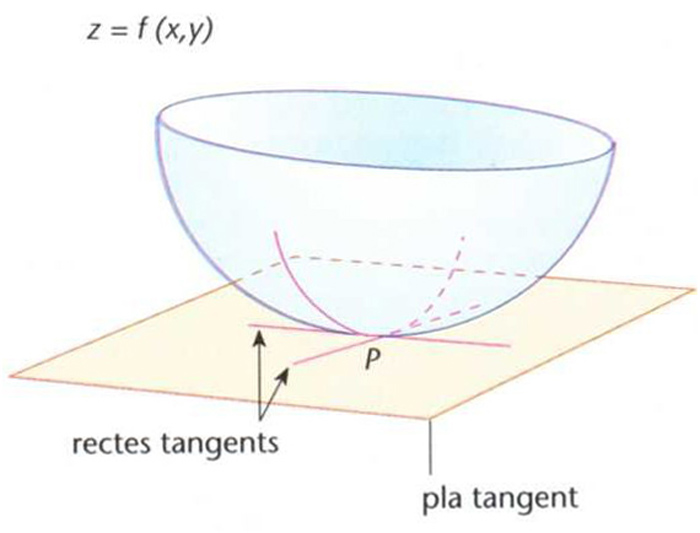
Pla tangent i dues rectes tangents a la superfície z= f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Donada una superfície z=f(x,y) i un punt P [x0, y0f(x0, y0)], pla que conté les rectes tangents en aquest punt a totes les corbes contingudes en la superfície considerada i que passen pel punt [x0, y0, f(x0, y0)].
L’equació d’aquest pla és
teorema de Desargues
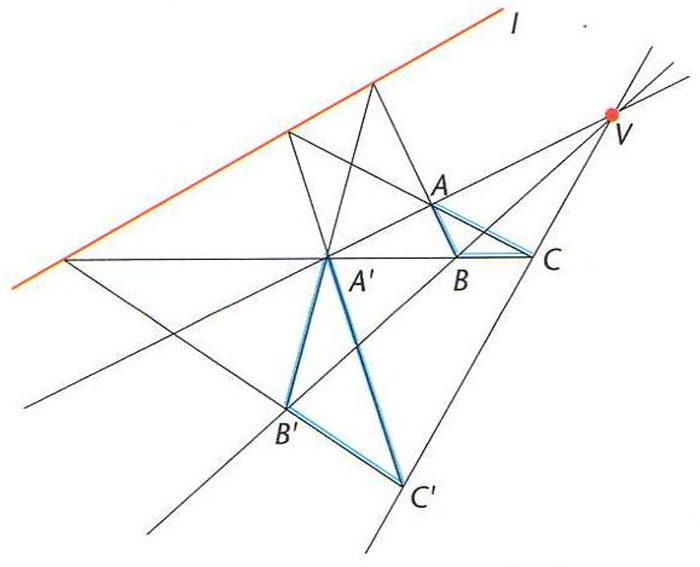
V és el punt de concurrència de les rectes AA’, BB' i CC' i l és la línia que conté els punts de concurrència de AB i A'B', de BC i B'C' i de CA i C'A'
© fototeca.cat
Matemàtiques
Teorema segons el qual, donats dos triangles ABC i A’B’C’ tals que les rectes AA’, BB’ i CC’ són concurrents, els punts de concurrència de AB i A’B’, de BC i B’C’ i de CA i C’A’ són alineats.
funció tangent
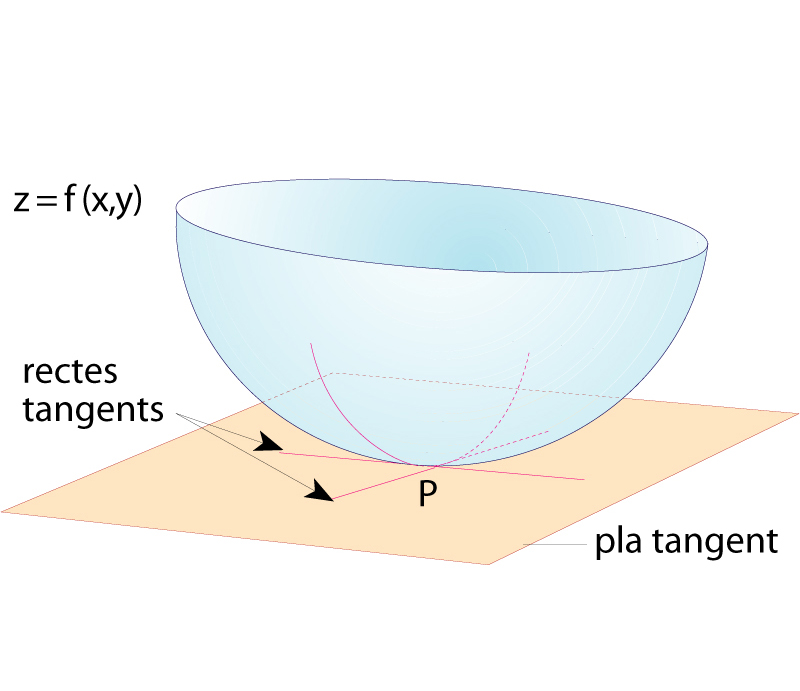
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
paral·lelisme
Matemàtiques
Qualitat de paral·lel.
La relació de parallelisme, definida tant en el conjunt de rectes com en el conjunt de plans, és una relació d’equivalència El conjunt quocient, en el cas de les rectes, és el conjunt de direccions
feix
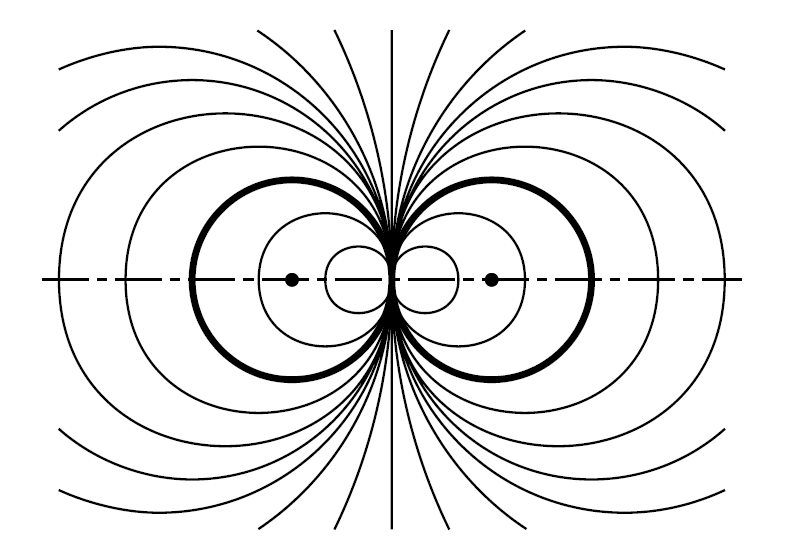
Feix de circumferències obtingudes a partir de dues circumferències iguals i tangents
Matemàtiques
Conjunt de superfícies o línies d’equació f + λφ = 0, f = 0 i φ = 0 essent les equacions de dos elements qualssevol del feix, els quals hom pren com a generatrius, i λ un paràmetre.
Tots els elements d’un feix tenen en comú la intersecció així, els plans d’un feix de plans tenen comuna la recta d’intersecció, i les rectes d’un feix de rectes, el punt d’intersecció
secció
Matemàtiques
Intersecció d’un pla amb una superfície.
Si aquesta és una superfície cònica, hom parla de seccions còniques ellipses, hipèrboles i paràboles, parells de rectes, etc Les seccions produïdes en prismes i cilindres per plans perpendiculars, respectivament, a les arestes laterals i a les generatrius, són anomenades seccions rectes
homotècia
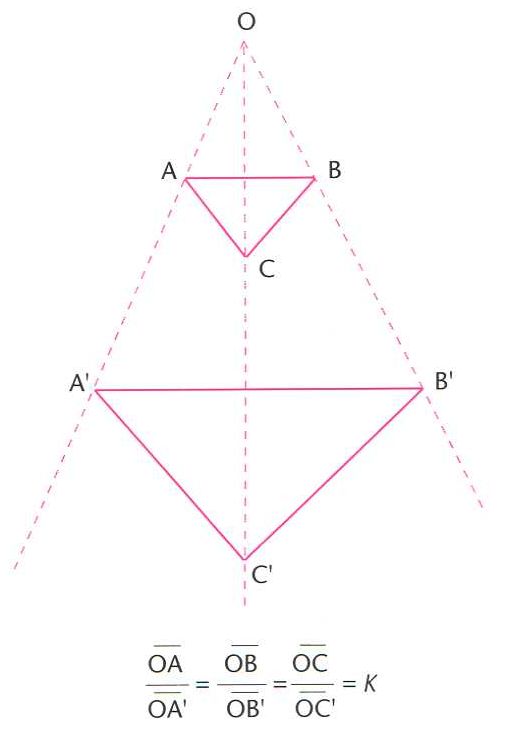
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
fórmula del trapezi
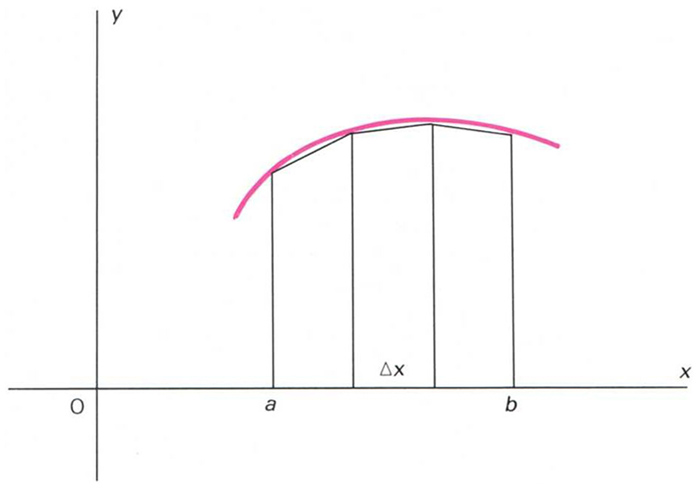
Aplicació de la fòrmula del trapezi
© fototeca.cat
Matemàtiques
Regla utilitzada per a aproximar l’àrea compresa entre una corba, una línia horitzontal i dues de verticals que tallen la corba.
Hom divideix el segment horitzontal en diverses parts iguals i dibuixa les perpendiculars des de cada punt de divisió a la corba després les interseccions d’aquestes rectes amb la corba són unides mitjançant línies rectes, successivament La suma de les àrees dels trapezis així engendrats representa una aproximació de l’àrea limitada per la corba