Resultats de la cerca
Es mostren 243 resultats
Pitàgores
Filosofia
Matemàtiques
Filòsof i matemàtic grec, fundador de l’escola o secta politicoreligiosa que porta el seu nom.
Malgrat la incertesa de les notícies que hom en té, sembla que s’establí, procedent de l’Àsia Menor, a Crotona ~530 aC, on fundà una comunitat ascètica centrada en l’estudi de les matemàtiques i activa en els afers polítics de la ciutat, i d’on, ja vell, hagué de fugir a la veïna Metapont arran d’una rebellió que hi tingué lloc La saviesa del mestre no fou divulgada pels seus deixebles, tal com establien els preceptes de la comunitat, motiu pel qual és difícil de destriar la part de les creences del pitagorisme que correspon a Pitàgores mateix i no a aportacions dels seus deixebles Sembla,…
equació integral
Matemàtiques
Equació on la funció que cal determinar es troba dins l’integrant d’una certa integral coneguda.
L’exemple més simple és l’equació , on la funció f x és coneguda i cal trobar la funció f x En virtut del teorema fonamental del càlcul, la solució és, en certes condicions de regularitat, Aquestes equacions les trobem en la resolució matemàtica de problemes físics i tècnics
lema de Zorn
Matemàtiques
Lema establert pel matemàtic nord-americà d’origen alemany Max Zorn, segons el qual en tot conjunt ordenat inductiu (és a dir, on tot subconjunt totalment ordenat té una fita superior) existeix un element maximal.
Aquest lema o axioma és “equivalent lògicament” a l' axioma de Zermelo i al teorema de Zermelo i d’altres d’enunciats L’ús del lema de Zorn és molt freqüent, en especial per a demostrar teoremes d’existència com ara el referent a la base d’un espai vectorial
fórmula de Boltzmann
Física
Expressió que relaciona l’entropia S d’un sistema (magnitud macroscòpica) i el nombre d’estats microscòpics accessibles pel sistema, W (magnitud microscòpica): S = k lnW, essent k la constant de Boltzmann.
Palesa la connexió entre la termodinàmica clàssica i la mecànica estadística Al zero absolut T = 0 K totes les partícules del sistema són a l’estat fonamental, de manera que W = 1 i, per tant, S = 0, la qual cosa és d’acord amb el tercer principi de la termodinàmica teorema de Nernst
axioma de Zermelo
Matemàtiques
Axioma segons el qual, donada una col·lecció de conjunts, existeix un ‘‘mètode’’ de designar un element particular de cada conjunt com un element ‘‘especial’’ d’aquest conjunt.
Aquest axioma, anomenat també axioma de l’elecció , és equivalent al teorema de Zermelo, segons el qual tot conjunt admet una relació d’ordre que en fa un conjunt ben ordenat Hi ha una versió més dèbil de l’axioma de l’elecció en el cas d’ésser finita la collecció de conjunts
Jean Meusnier de la Place
Física
Matemàtiques
Físic i matemàtic francès.
Collaborà amb Lavoisier en els cèlebres experiments que donaren lloc a la descomposició de l’aigua en oxigen i hidrogen i a la seva ulterior síntesi Continuà les investigacions matemàtiques de Monge en un estudi que féu sobre la curvatura de les superfícies hi ha el teorema que porta el seu nom
Menelau d’Alexandria
Matemàtiques
Matemàtic grec.
Fou el primer a separar la trigonometria de l’estereometria i l’astronomia Féu la primera definició de triangle esfèric i utilitzà la relació entre els triangles esfèrics i els plans per a resoldre els triangles esfèrics teorema de Menelau Escriví el tractat Esfèrica , on establí els fonaments de la trigonometria esfèrica
tercer principi de la termodinàmica
Física
Principi segons el qual en el zero absolut de temperatura la variació d’entropia d’un sistema en un procés isotèrmic tendeix a zero.
Aquest principi emana del teorema de Nernst, enunciat el 1906 i completat per Planck el 1912 amb la hipòtesi que en el zero absolut l’entropia de qualsevol substància sòlida o líquida pura és zero Una conseqüència del tercer principi és que el zero absolut no es pot atènyer amb un nombre finit de transformacions termodinàmiques
desenvolupament en sèrie
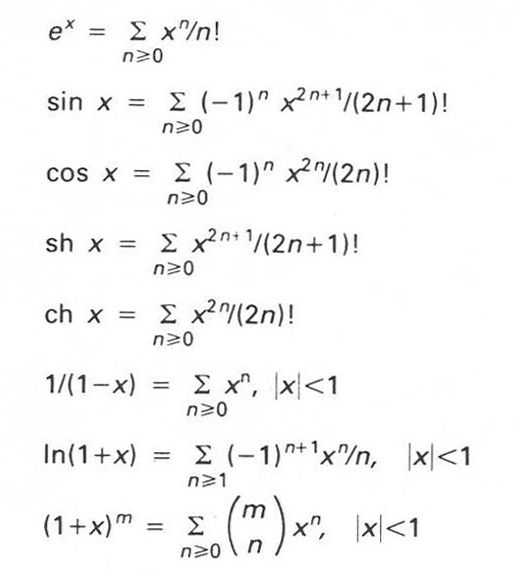
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
George Gabriel Stokes
Física
Matemàtiques
Matemàtic i físic irlandès.
Estudià la dinàmica dels fluids i establí la llei que duu el seu nom Investigà també la fluorescència i la difracció de la llum, en el qual camp enuncià una llei coneguda també amb el seu nom Com a matemàtic formulà un teorema sobre les integrals de superfície 1849 i estudià la convergència de les sèries
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- …
- Pàgina següent
- Última pàgina