Resultats de la cerca
Es mostren 284 resultats
avet de Douglas

Avet de Douglas
Jamain (cc-by-sa-3.0)
Botànica
Arbre de la família de les pinàcies, semblant a l’avet de fulles sempre verdes, d’uns 2-3,5 cm de llargada; les pinyes són d’un bru brillant, pèndules, de 5 a 10 cm de longitud.
En condicions òptimes l’avet de Douglas arriba a tenir fins a 100 m d’alçària, amb un tronc de 12 m de circumferència Es fa en extenses zones de l’oest nord-americà És plantat sovint a les terres humides d’Europa com a arbre forestal
bruixa d’Agnesi
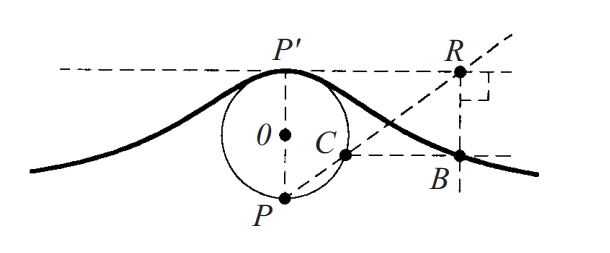
bruixa d’Agnesi
© Fototeca.cat
Matemàtiques
Cúbica plana generada a partir d'una circunferència, un punt P d'aquesta i la tangent en el punt diametralment oposat a P.
Cada recta traçada per P talla la circumferència en un punt C , i la tangent en un punt R La corba és el lloc dels punts d'intersecció de la perpendicular per R a la tangent amb la parellela a aquesta tangent traçada des de C
Superconducting Supercollider
Supercol·lisionador superconductor de protons contra protons que es va intentar construir a Wahaahtchee, a 40 km al sud de Dallas, amb un pressupost de 9 000 milions de dòlars.
Amb 87 quilòmetres de circumferència, havia de ser el més gran del món, probablement no superat per cap altra installació d’aquest tipus Havia d’assolir una energia de 20 TeV Estava previst que comencés a funcionar l’any 1996, però fou cancellat el 1993 per problemes pressupostaris
superfície de revolució
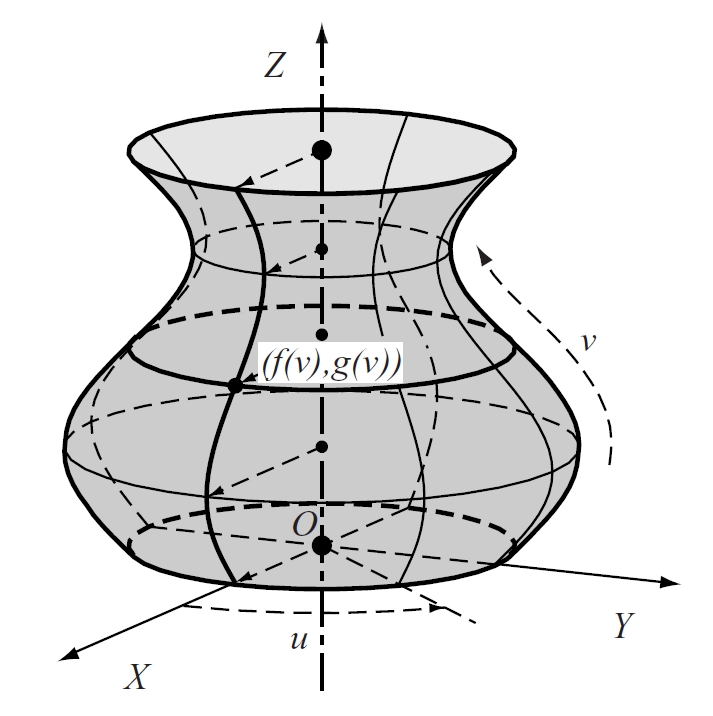
Superfície de revolució
Matemàtiques
Superfície engendrada per la rotació d’una corba (generatriu) entorn d’un eix, anomenat de revolució.
Si aquesta corba és plana i situada en un pla que conté l’eix és anomenada meridiana de la superfície La circumferència descrita per cada punt de la meridiana és anomenada parallel Els meridians i els parallels d’una superfície esfèrica són circumferències Els meridians de la superfície terrestre són aproximadament ellipses
Hera
Accelerador de partícules inaugurat a Hamburg el 1991.
Finançat per Alemanya i amb la participació de França, té sis quilòmetres de circumferència i s’hi produeixen collisions de protons i electrons és l’única installació del món que produeix aquests xocs Amb 10 milions de collisions per segon i una energia de 320 GeV, permet estudiar l’estructura interna dels protons, és a dir, els quarks
zona de borneig
Transports
Espai necessari per a bornar un vaixell.
Quan aquest és fondejat amb una sola àncora o subjectat a un cos mort, la zona de borneig és una circumferència amb centre en un punt de la cadena de l’àncora, o l’àncora mateixa Quan és fondejat amb més d’una àncora, és la resultant de les corresponents a cada una de les àncores, i, per tant, més reduïda
tevatró
Física
Sincrotró del Laboratori Nacional Fermi, Illinois, EUA.
Fou acabat de construïr el 1983 i estigué actiu fins el 2011 Arribà a proporcionar energies de fins 0,98 TeV a cada raig de protons o antiprotons circulant en el seu interior fins a 1,96 TeV en la seva collisió Té 6,28 km de circumferència El seu nom prové de la unitat d’energia que podia assolir, el teraelectronvolt TeV
corbes de Lissajous
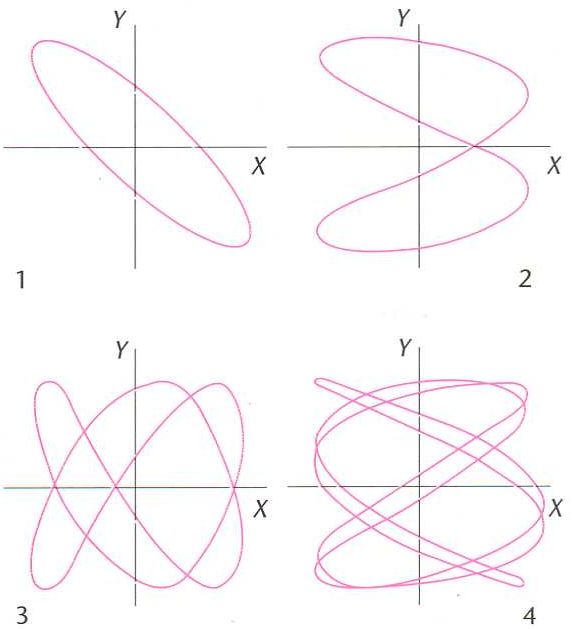
Corbes de Lissajous la relació entre les pulsacions wx i wy dels dos moviments corresponents.
© Fototeca.cat
Matemàtiques
Corbes que apareixen en la composició de dos moviments vibratoris harmònics perpendiculars entre ells.
Hom obté corbes molt diverses, en general obertes, però, si la relació entre els períodes dels dos moviments és racional, la corba obtinguda és tancada i el moviment resultant és periòdic si els dos períodes són iguals, la corba resultant és una circumferència o una ellipse Hom les pot reproduir fàcilment en un oscilloscopi fent que les tensions horitzontal i vertical siguin sinusoidals
Tevatron
Sincrotró del Laboratori Nacional Fermi, Illinois, EUA.
Fou acabat de construïr el 1983 i estigué actiu fins el 2011 Arribà a proporcionar energies de fins 0,98 TeV a cada raig de protons o antiprotons circulant en el seu interior fins a 1,96 TeV en la seva co»isió Té 6,28 km de circumferència El seu nom prové de la unitat d’energia que podia assolir, el teraelectronvolt TeV
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- …
- Pàgina següent
- Última pàgina