Resultats de la cerca
Es mostren 578 resultats
multiplicació
Matemàtiques
Operació aritmètica que, donats dos nombres naturals a (el multiplicand) i b (el multiplicador), consisteix a trobar un nombre, ab, a × b o a · b, que és el resultat de sumar b vegades el nombre a
.
En teoria de conjunts, hom defineix el nombre ab com el cardinal del producte cartesià A × B , on A és un conjunt de cardinal a , i B un conjunt de cardinal b La multiplicació és anomenada també producte i gaudeix de les propietats associativa, commutativa i distributiva respecte a la suma En les successives extensions del conjunt de nombres naturals fins a arribar als nombres complexos, hom va generalitzant convenientment la definició de la multiplicació, sense perdre, però, cap de les propietats anteriors ni tampoc la propietat que l’element neutre es pot anar identificant sempre amb el…
equació diofàntica
Matemàtiques
Equació algèbrica els coeficients de la qual són nombres enters i en la qual hom tracta de determinar els valors enters de les variables que satisfan les dites equacions.
També s’estudien problemes diofàntics en el conjunt dels nombres racionals o en l’anell d’enters d’un cos
mitjana
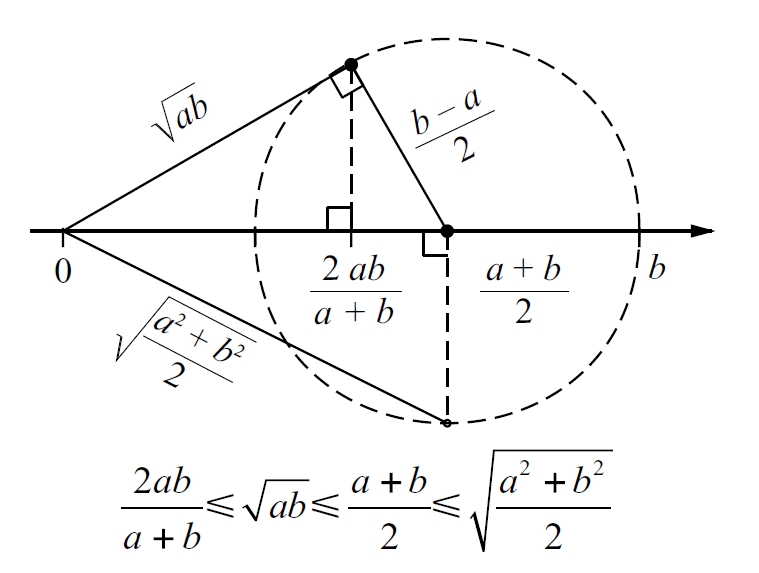
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de la mitjana és…
enter
Matemàtiques
Classe d’equivalència que la relació (a,b)R(c,d), si, i només si, a+d = b+c, indueix en el conjunt producte ℕ × ℕ (ℕ essent el conjunt dels nombres naturals).
El conjunt d’aquestes classes d’equivalència conjunt quocient és el conjunt dels nombres enters ℤ = {0, ±1, ±2, ±3, } Hom anomena representant canònic d’un enter a,b aquell en què o a o b és 0 Si l’esmentat representant canònic és de la forma m, 0, aquest és un enter positiu , representat també per + m si és la forma 0, m , es tracta d’un enter negatiu , habitualment representat per - m i si és 0,0, és l' enter nul , o sigui 0 En el conjunt ℤ hom defineix dues operacions la suma és definida per a, b + c, d = a + c , b + d , i el producte , per a, b c, d = ac + bd, ad + bc Tal…
successions de Fibonacci
Matemàtiques
Successions de nombres enters positius, (un)n≥₀, donades per la llei de recurrència un=un-₁ + un-₂, n≥2.
Les diferents successions resulten d’una elecció concreta dels dos primers termes u₀ i u₁ Hom anomena, generalment, successió de Fibonacci aquella que fa u₀ = u₁ =1, la qual té per terme general i els primers termes de la qual són 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,, anomenats nombres de Fibonacci Aquesta successió de Fibonacci té propietats força interessants u n =Σ i j , on el sumatori s’estén per als índexs tals que i - j = n i j ≤ n u n i u n - ₁ són primers entre ells que és el nombre d’or Hom ha definit també successions de Fibonacci generalitzades , donades per u₀ = a, u₁ = b i per…
polinomi
Matemàtiques
Suma formal de productes de nombres, anomenats coeficients (reals, complexos o, més generalment, elements de qualsevol anell) per elements anomenats variables (generalment denotats per x, y, z, etc), als quals hom atribueix només les propietats algèbriques més simples.
Usant aquestes propietats hom defineix la suma i el producte de polinomis, de manera que els polinomis de n variables formen una àlgebra Substituint les variables per nombres hom obté una funció anomenada funció polinòmica
regla de falsa posició
Matemàtiques
Mètode per a resoldre l’equació a x = b, utilitzat abans d’ésser inventada la notació algèbrica actual, consistent a utilizar la fórmula (escrita en la notació actual) on x1 i x2 són nombres tals que .
La regla, doncs, era aplicada determinant dos nombres x 1 , x 2 tals que a x 1 i a x 2 superessin b i determinant a continuació les diferències d 1 i d 2 abans de determinar x Aquesta regla, que fou introduïda a Europa pels àrabs, probablement procedia de la Xina
sistema de coordenades
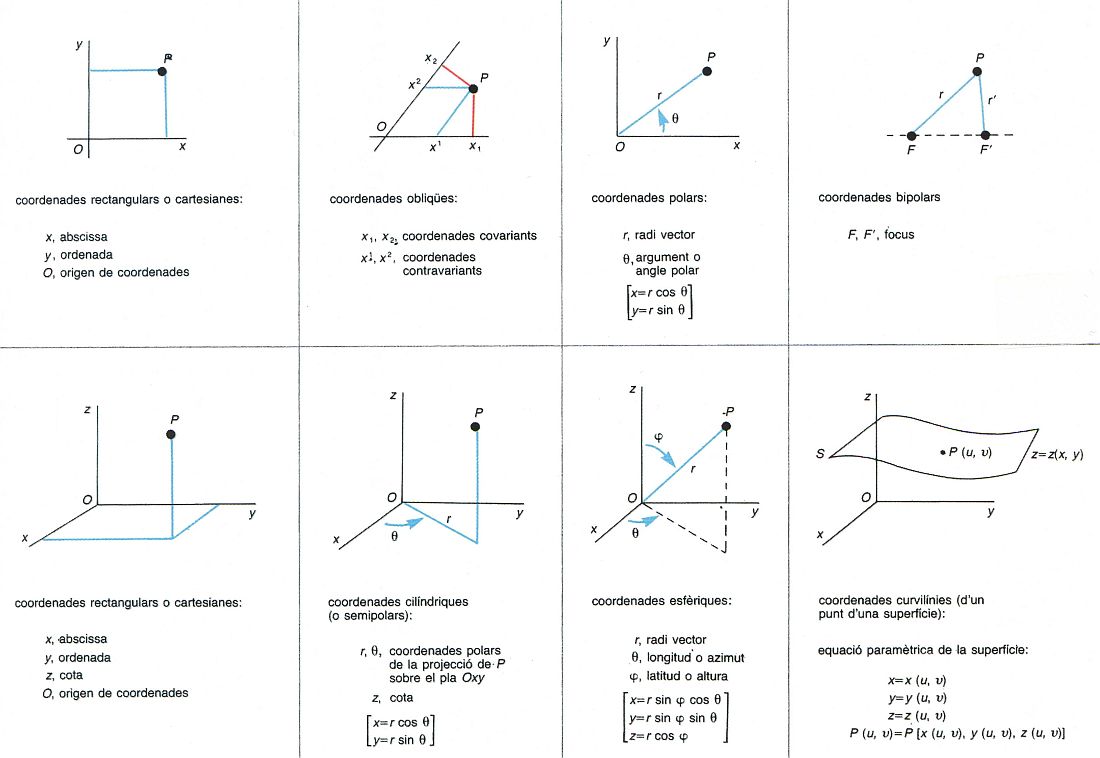
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot considerar les coordenades covariants o contravariants , que…
piràmide ecològica
Ecologia
Diagrama de forma generalment piramidal en el qual hom representa la biomassa, els nivells d’energia o els nombres dels organismes de cada nivell tròfic d’un ecosistema.
Els organismes productors fotosintetitzadors ocupen la base de la piràmide Per sobre d’aquests hi ha successivament les diverses menes de consumidors fitòfags, carnívors depredadors d’herbívors i carnívors depredadors de carnívors Cada nivell tròfic de l’ecosistema es manté mercès a l’energia que obté del nivell immediatament inferior cada nivell tròfic té una producció més gran que el seu nivell immediatament superior i més petita que el seu nivell inferior, ja que cada nivell superior és explotat amb menys intensitat, cadascun determinat per la seva biomassa i la seva producció El nombre de…
nombre natural
Matemàtiques
Nombre que serveix per a comptar els elements d’un conjunt.
La manera més freqüent de representar els nombres naturals és el sistema de numeració decimal, i el conjunt dels nombres naturals acostuma a ésser representat amb la lletra ℕ En la concepció dels nombres naturals, i també de les altres menes de nombres, hom pot donar prioritat a l’aspecte intuïtiu o a l’aspecte lògic Des del punt de vista intuïtiu, un nombre natural és una qualitat dels conjunts equipotents així, la classe de tots els conjunts equipotents amb el conjunt { X o Δ} és el nombre tres L’operació “unió de conjunts sense elements comuns” engendra l’operació de “sumar nombres…
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- …
- Pàgina següent
- Última pàgina