El mètode dóna, a més, el polinomi p(x)/(x-a), i així, d’una forma successiva, hom pot arribar per reiteració a determinar totes les solucions reals del polinomi. És, però, un mètode de comprovació i no pas un algorisme de resolució. El mètode és el següent: sigui, per exemple, el polinomi x2 + x - 2; hom escriu els coeficients 1, 1, -2, i a continuació, suposat un valor qualsevol escollit entre els divisors del coeficient independent (que en aquest cas és -2), per exemple 1, hom fa els càlculs següents:
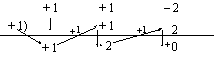
És a dir, el primer coeficient resta igual; al segon hom suma el producte del primer coeficient pel valor suposat; al tercer suma el producte del valor anterior pel valor suposat, etc. Si el darrer càlcul dóna zero, aleshores el valor suposat és una solució. En l’exemple +1 és una solució i, per tant, (x - 1) divideix el polinomi x2 + x - 2. El polinomi quocient és el que té precisament com a coeficients els obtinguts per l’aplicació de la regla (+1, +2) i amb un grau inferior, és a dir, x + 2. Aquest mètode és d’especial utilitat amb polinomis de grau superior a tres, perquè la resolució és molt complicada, i sobretot en el cas d’un grau superior a cinc, en què no existeix tal resolució algèbrica per quadratures.