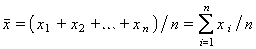La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà. Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població, mentre que si les observacions són d’una mostra aleatòria de la població (mostreig), x és la mitjana de la mostra. A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra. Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n1, n2, ..., nk i freqüències respectives f1, f2, ..., fk, la fórmula per al càlcul de la mitjana és
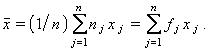
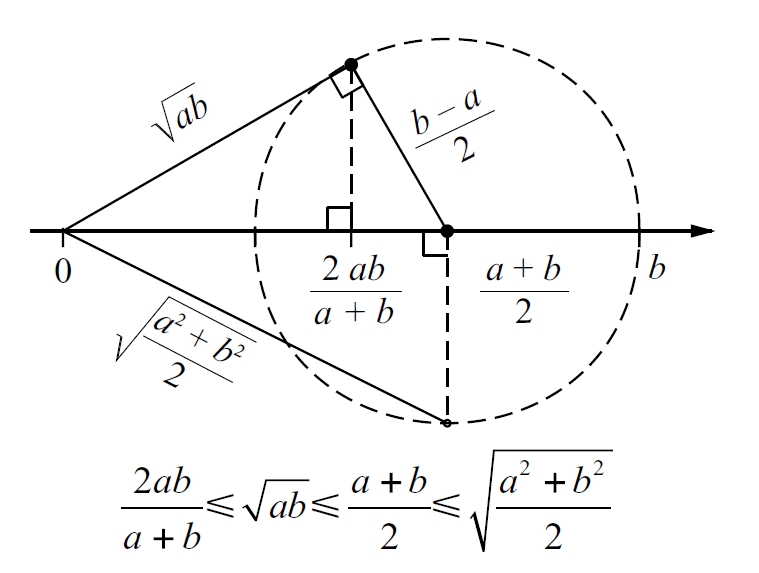
Cal no confondre aquesta expressió amb la de la mitjana ponderada, en la qual els coeficients de les xj són els coeficients de ponderació en lloc de les freqüències. Si és una distribució teòrica, les fj seran substituïdes per les probabilitats teòriques, i en aquest cas la mitjana és anomenada esperança matemàtica de la distribució. Tot i que la mitjana aritmètica té propietats matemàtiques que la fan de bon manipular i és la més utilitzada, hi ha altres definicions de mitjana, com la mitjana geomètrica, que és l’arrel enèsima del producte de les observacions, la mitjana harmònica, que és la recíproca de la mitjana aritmètica dels recíprocs de les observacions, i la mitjana quadràtica, que és l’arrel quadrada de la mitjana aritmètica dels quadrats de les observacions.