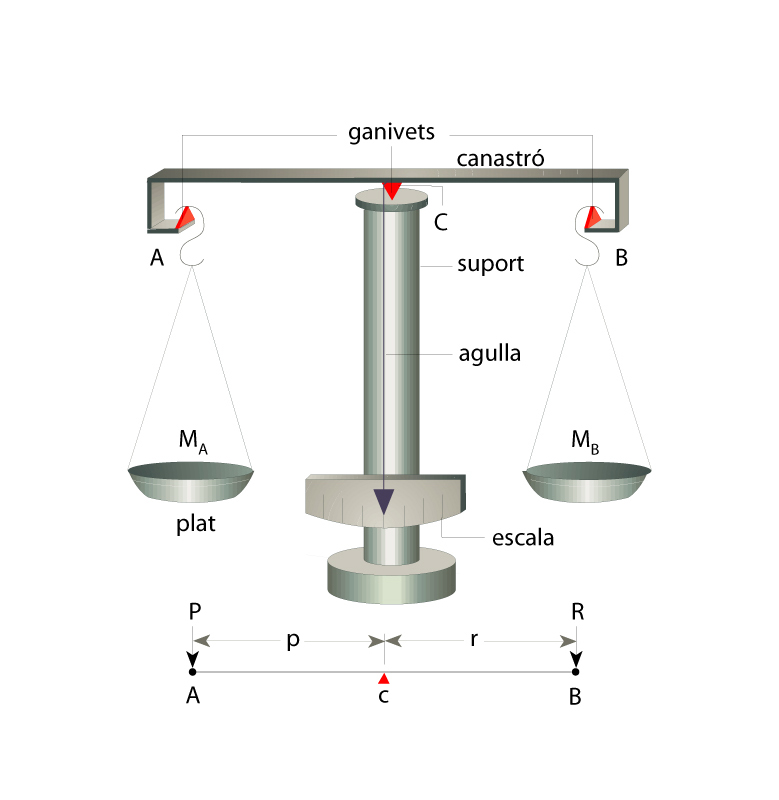
El tipus bàsic és el de la balança que té els braços d’igual longitud, o balança de braços iguals. Aquesta, en esquema, és formada per una barra rígida anomenada canastró, que és travessada transversalment per tres prismes d’acer anomenats fulcres. L’aresta inferior, o ganivet, del fulcre central del canastró recolza sobre una superfície horitzontal dura (d’àgata o acer), que forma part del suport fix de la balança, i materialitza així un eix horitzontal i perpendicular al canastró, al voltant del qual aquest pot oscil·lar. Damunt els ganivets dels fulcres extrems del canastró recolzen dues plaques dures, de les quals pengen els dos plats o balançons, idealment iguals, destinats a sostenir les masses que hom compara. L’agulla de la balança, solidària i normal al canastró, es desplaça davant d’una escala el centre de la qual ha de correspondre a la posició d’equilibri, posició assolida quan les masses comparades són iguals. El funcionament d’una balança es basa en el principi de la palanca; de fet, una balança és una palanca de primer gènere en què una de les masses fa de resistència i el pes de l’altra actua com a potència. Per tal de fer correctament una pesada, cal d’antuvi despenjar els plats de llurs suports. Així, l’equilibri és assolit quan el centre de gravetat G del canastró és damunt la vertical de l’eix C. Hom comprova aleshores que els ganivets dels tres fulcres C, C1 i C2 siguin en un mateix pla horitzontal, moment en el qual hom fa que l’agulla de la balança assenyali el zero de l’escala. En col·locar els plats, la suspensió lliure i sense sol·licitacions d’aquests permet d’assegurar que es disposen de forma que llurs centres de gravetat cauen damunt les verticals de C1 i C2, respectivament. La balança ha d’ésser ajustada per tal que, en penjar els plats, romangui la situació inicial d’equilibri, l’agulla mantenint-se sobre el zero. Això s’acompleix si els corresponents moments rotatoris s’equilibren: p1l1 = p2l2 (p1, p2 pesos dels plats; l1, l2 distàncies CC1 i CC2). En carregar-hi les masses M1 i M2 a comparar, la mateixa suspensió lliure assegura que els centres de gravetat dels sistemes m1 + M1 i m2 + M2 (m1 i m2 masses dels plats) són damunt les verticals de C1 i C2, respectivament; en conseqüència, els pesos s’apliquen sempre sobre aquests punts i els braços de palanca són sempre els mateixos, l1 i l2. Hom diu que les masses M1 i M2 són iguals, si els consegüents moments rotatoris s’equilibren: (p1 + P1) l1 = (p2 + P2) l2, essent P1 i P2 els pesos de les masses M1 i M2 ; atès que, per construcció, p1l1 = p2l2, resulta aleshores que P1l1 = P2l2, és a dir, M1l1 = M2l2. Del grau d’igualtat de les distàncies l1 i l2 depèn que la balança apreciï més o menys exactament la igualtat de les masses M1 i M2. Si les masses són diferents, el canastró gira al voltant de C per efecte dels moments rotatoris de les forces p1 + P1, p 2 + P2 i P (el pes del canastró), fins que assoleix novament l’equilibri, en què forma un angle α amb l’horitzontal; així estant, es satisfà que (p1 + P81) l1 cos α = (p2P2) l2 cos α + Pd sin α. Si P2 és conegut (com és el cas d’una pesada amb masses conegudes), l’escala graduada permet d’assignar a cada valor d’α el corresponent pes P1.
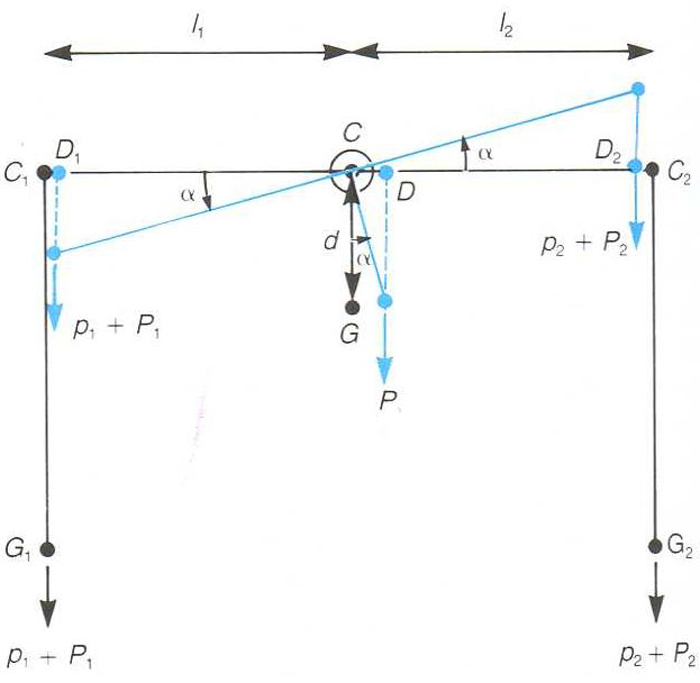
Funcionament d’una balança de braços iguals; en negre, disposició quan les masses són iguals, i en blau, quan són diferents
© Fototeca.cat
Com en tot altre instrument de mesura, la bondat (o exactitud) de la balança és donada pels criteris de fidelitat, justesa i sensibilitat (o precisió). La fidelitat d’una balança mesura el grau en què és conseqüent en donar un mateix valor per a una sèrie de determinacions d’una mateixa massa. Bàsicament, la fidelitat depèn del paral·lelisme entre els ganivets dels fulcres C, C1 i C2, i de la rigidesa del canastró. Són corrents les balances que, preparades per a càrregues no superiors a 200 g, són fidels amb un grau d’indeterminació de 0,1 mg. Hom diu que una balança és justa quan, trobant-se en l’equilibri, aquest no es modifica per la col·locació en cada platet d’una massa idèntica. De l’expressió d’aquest equilibri, pl1 = pl2, essent p el pes de la massa afegida a cada platet, hom dedueix que la justesa és funció del grau d’igualtat entre les longituds dels braços. Si una balança és justa, la massa d’un cos es determina simplement equilibrant-la mitjançant masses conegudes, mètode aquest anomenat de simple pesada. Per tal de comprovar la justesa, cal canviar de plats les masses i assegurar-se que l’equilibri roman.
Ajustament i sensibilitat de les balances. Història de les balances
Una balança no és mai absolutament justa, de manera que, si P1 i P2 són els pesos que hom afegeix als respectius plats per aconseguir que l’equilibri no variï, aleshores P1l1 = P2l2 i, per tant, (P1— P2)/ P1 = (l2= l1)/ l2. D’aquesta expressió es dedueix que per a obtenir una exactitud de 0,1 mg sobre 200 g en una balança de 100 mm de braç, la diferència de longitud entre els braços ha d’ésser de 0,5 x 10-4 mm. L’obtenció d’una diferència tan petita és pràcticament impossible, puix que és suficient una petita diferència de temperatura en l’ambient que envolta el canastró per a produir aquestes diferències de longitud. Hom eludeix el problema fent servir mètodes que permeten d’eliminar la influència de les causes externes a l’estructura pròpia de la balança. Per exemple, el mètode de la doble pesada (o de Borda) consisteix a col·locar un pes conegut P en un plat i el cos a pesar p a l’altre. Mitjançant pesos suplementaris P2 afegits a aquests, hom aconsegueix l’equilibri: Pl1 = (p + P2) l2. Substituint els pesos del segon plat per un altre pes conegut P2’, l’equilibri assolit indica que Pl1 = P2’l2, d’on resulta que p = P2’ — P2. Hom pot definir la sensibilitat (o precisió) d’una balança donant els valors de la sobrecàrrega més petita que, aplicada sobre un dels platets, produeix un desplaçament perceptible de l’agulla. D’aquesta manera, hom fa dependre la sensibilitat directament del sistema amb el qual és observat el moviment de l’agulla; així, doncs, hom pot dir que la sensibilitat d’una balança és una o una altra de molt més gran, segons que hom l’observi de manera directa, sense utilitzar aparells, o fent ús d’un microscopi o d’un nònius. L’observació feta a través d’un aparell pot arribar a donar valors de la sensibilitat superiors a la fidelitat. Hom prefereix de donar la sensibilitat fent ús només de les propietats mecàniques i partint de la posició d’equilibri. Si l’equilibri ve donat per (p1+ P1) l1 = (p2+ P2) l2, en afegir la sobrecàrrega p el canastró gira un angle α i, en obtenir l’equilibri, se satisfà que (p1+ P1+ p) l1 cos α = (p2+ P2) l2 cos α + P d sin α, essent P el pes del canastró i d la distància CG. D’aquestes dues equacions resulta que tg α = pl1, de manera que, donada p, l’angle α augmenta conforme disminueixen d i P. Per tal d’aconseguir la màxima sensibilitat és convenient de construir el canastró del material més lleuger possible, de la forma menys deformable i amb els braços de la longitud mínima, obligada només per l’espai necessari als platets. Per a sobrecàrregues petites, α = σp, on σ = l1/ dP és la sensibilitat. Les balances foren conegudes en les civilitzacions urbanes del Próxim Orient, tant a Mesopotàmia com a Egipte, on apareixen sovint representades en les escenes funeràries pesant l’ànima dels morts. Pertanyen al tipus de balança de braços iguals, suportada per una columna. Hom coneix els sistemes de pesos de les civilitzacions del Pròxim Orient, relacionats directament amb l’ús normal de les balances. L’extensió d’aquest ús anà molt lligada amb la necessitat de pesar metalls (or, argent, bronze) com a elements bàsics de l’intercanvi comercial. D’ençà de l’invent de la moneda i gairebé fins a l’època actual, la balança ha estat indispensable per tal d’assegurar la correspondència entre el pes i el valor teòric de les monedes, sobretot les d’or. Al món grecoromà foren emprats dos tipus de balança. La balança de braços iguals, de bronze o de ferro, fou anomenada en llatí libra, i en llatí tardà bilancia, de bis (dos) i lanx (plat). A les terres catalanes hom ha trobat plats de balança de bronze i pesos a diversos poblats ibèrics d’èpoques anteriors a la conquesta romana. L’altre tipus de balança en ús al món clàssic fou l’actualment anomenada romana (statér en grec; statera en llatí), de la qual es conserven nombrosos exemplars a tot el món romà, sobretot de les de mida petita, fetes de bronze, i de les quals també hi ha troballes als Països Catalans. Aquests dos tipus de balances perduren gairebé sense cap variant i s’han mantingut fins ara. Fins entrat el segle XIX no aparegueren models diferents, derivats de canvis provocats per la revolució industrial, com la bàscula, la balança de Roberval, la balança de Béranger o de caixa i l’automàtica, així com les diferents balances de laboratori.