La noció de fase generalitza la d’estat físic (sòlid, líquid, gasós) i permet distincions més subtils, com la que hi ha entre dues formes de cristal·lització d’un sòlid. Els components d’un sistema són les substàncies que l’integren, i els constituents són les diferents fases que el formen. Si només hi ha una fase, el sistema és homogeni, i si n'hi ha més, heterogeni . El pas de la fase sòlida a la líquida és anomenat fusió , el de la líquida a la gasosa, vaporització , i el de la sòlida a la gasosa, sublimació . Aquests canvis de fase són progressius, i els canvis en sentit contrari són anomenats regressius ( solidificació, liqüefacció i solidificació ). En sistemes d’un sol component ( sistemes unaris ), els canvis de fase segueixen dues lleis, anomenades de canvis de fase : la primera diu que a una pressió exterior determinada el canvi progressiu i el regressiu corresponent ocorren a la mateixa temperatura, i la segona, que en un canvi progressiu el sistema absorbeix una quantitat de calor per unitat de massa (dita calor del canvi ), i en el regressiu desprèn la mateixa quantitat de calor, si els canvis tenen lloc a la mateixa pressió exterior. Aquestes lleis es dedueixen dels principis de la termodinàmica. En particular, quan en sistemes d’un sol component coexisteixen dues fases en equilibri, l’energia lliure molar d’ambdues fases és la mateixa. D’aquest fet hom dedueix l’equació de Clapeyron:
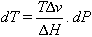
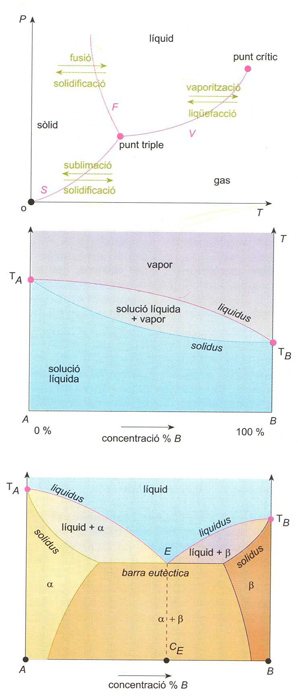
que dóna la variació dT de la temperatura T del canvi de fase en variar la pressió exterior dP, ΔH essent la calor molar del canvi i Δν la variació del volum molar en el canvi; aquesta equació permet de preveure fets com ara la possibilitat de fondre glaç per pressió (puix que a l’aigua és Δν = 0). Hom sol representar les diferents fases d’un sistema d’un sol component en un diagrama, anomenat diagrama de fases o diagrama d’equilibri , on les corbes indiquen les condicions ( p, T ) en què hi ha equilibri entre dues fases. Aquestes corbes corresponen als estats dels sistemes monovariants (dues fases en equilibri) i separen les zones dels sistemes bivariants (estabilitat d’una sola fase). L’equació de Clapeyron escrita en la forma dP/dT = Δ H/( T Δν) dóna el pendent d’aquestes corbes. El punt on es tallen és l’anomenat punt triple , i indica les condicions de pressió i de temperatura per a les quals coexisteixen les tres fases del sistema. La corba de vaporització acaba en el punt crític. En sistemes de més d’un component, l’equilibri entre fases és aconseguit quan el potencial químic de cada component és el mateix en les diferents fases en què es troba. Aquestes condicions fixen uns graus de llibertat del sistema (en els d’un component només hi havia una condició sobre l’energia lliure, que és un cas particular d’aquestes noves condicions), de manera que el nombre V dels que no resten fixats, nombre anomenat variància , depèn del nombre de components C i del de fases P , segons la regla de les fases: V =C—P +2.
Per exemple, segons aquesta regla, la variància en el punt triple d’un sistema d’un sol component és nul·la. Amb l’ajut d’aquesta regla, enunciada per Gibbs el 1875, hom construeix el diagrama de fases o diagrama d’equilibri , per a cada sistema. En el cas dels sistemes de dos components ( binaris ), el diagrama complet exigiria tres dimensions. Limitant-se a dues, hom representa les mateixes variables per una composició fixa o bé, més útilment, en fixa una (la pressió, en general) i representa l’altra (la temperatura, en general) en ordenades, en funció de la composició, en abscisses. El diagrama indica aleshores, per a cada temperatura i composició, si el sistema és constituït per una sola fase o si dues fases hi són en equilibri. Hom classifica els sistemes líquid-líquid fonamentalment en dos tipus: els sistemes no azeotròpics , amb un augment regular del punt d’ebullició en variar la composició del sistema per enriquiment en el component menys volàtil, i els sistemes azeotròpics , que presenten un punt d’ebullició màxim o mínim. Els sistemes sòlid-líquid poden ésser classificats en sistemes no eutèctics, que formen una sèrie contínua de dissolucions sòlides, en els quals el punt de congelació del sistema varia entre els dels dos components del sistema o, en alguns casos, presenta un màxim o un mínim, i en sistemes eutèctics , que presenten el fenomen d' eutèxia , en els quals, en disminuir la temperatura i per a una composició inicial determinada, es diposita una de les fases sòlides i s’enriqueix la dissolució en l’altre, fins que, en arribar a una composició determinada ( composició eutèctica ), es precipiten ambdues fases sòlides juntes. L’estudi dels punts eutèctics té un gran interès en la metal·lúrgia, puix que permet de determinar la composició dels composts intermetàl·lics que es formen en els aliatges. En el cas dels sistemes de tres components ( ternaris ), una forma corrent de diagrama és el diagrama triangular , en el qual cada component pur va representat per un vèrtex d’un triangle equilàter. Cada costat representa aleshores un sistema binari, i els punts a l’interior del triangle, sistemes ternaris. Si hom suposa la pressió fixa, la variació de la temperatura és representada per una perpendicular al pla del triangle i hom obté una figura de tres dimensions constituïda per superfícies —que representen l’equilibri entre dues fases (sistemes trivariants)—, llurs línies d’intersecció —representen equilibris entre tres fases (sistemes bivariants)— i els punts d’intersecció —equilibris entre quatre fases (sistemes monovariants)—. Representant bidimensionalment, a l’interior del triangle, les projeccions de les interseccions entre les superfícies esmentades hom obté una projecció politèrmica , i tallant la figura tridimensional per plans paral·lels al triangle de base, seccions isotèrmiques.