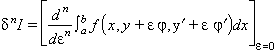El problema consisteix a determinar les variables dependents, de manera que la integral sigui màxima o mínima. En el cas més simple, la integral és de la forma
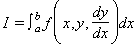
on cal determinar la funció y(x) de manera que I sigui màxima o mínima. També poden ésser considerades integrals de la forma
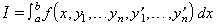
on y1, ..., ynsón funcions de x desconegudes o bé integrals múltiples tals com
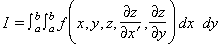
on z =z(x,y) és desconeguda; com també poden ser-ho com integrals múltiples d’ordre superior o de diverses variables dependents. L’integrant pot ésser també una funció en la qual intervinguin derivades parcials d’ordre superior. En el càlcul de variacions, la variació δy(x) d’una funció y(x) és qualsevol funció δy(x) que pugui sumar a y(x) per a donar una nova funció y(x)+ δy(x). El nom de “càlcul de variacions” fou adoptat a causa d’aquesta notació, introduïda per Lagrange cap a l’any 1760 en comparar el valor d’una integral al llarg d’un arc de corba amb el seu valor al llarg d’un arc proper. Hom defineix la variació primera d’una integral I = ∫baf (x,y,y’) dx, mitjançant
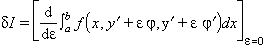
sempre que existeixi per a certes variacions Ω(x) de y(x). En el cas que Ω(a) = Ω(b) = 0, aleshores
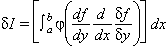
En general, la variació enèsima de I és definida així: