Sigui E un espai vectorial sobre un cos commutatiu K, per a cada parella (p, q) de nombres naturals, existeix una aplicació bilineal única Tpq de Tp (E) X Tq (E) en Tp+q (E) tal que, per a tot element (x1,..., xp) d’Ep i tot element (xp+1,..., xp+q) d’Eq, Tpq (x1 OOOoooOOO xp, xp+1 OOOoooOOO xp + q) = x1 OOOoooOOO xp+q, on T n (E) és la potència tensorial n -èsima d E. Les aplicacions bilineals Tpq defineixen sobre l’espai vectorial
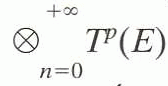
una estructura de K -àlgebra graduada. És l’àlgebra tensorial de l’espai vectorial E i és designat T (E)