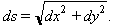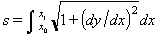Usualment també designa una corba oberta completa. Les característiques d’un arc (llargada, corda, fletxa) depenen de la corba a la qual pertany. En el cas d’una circumferència, hom mesura els arcs en unitats d'angle i un arc val igual que l'angle en el centre que el limita (en trigonometria, però, hom considera a vegades que un arc de circumferència α, mesurat en radians, admet una infinitat de determinacions que difereixen per un nombre enter de circumferències i són donades per la fórmula α + 2kπ, on k pot ésser zero o un enter qualsevol).
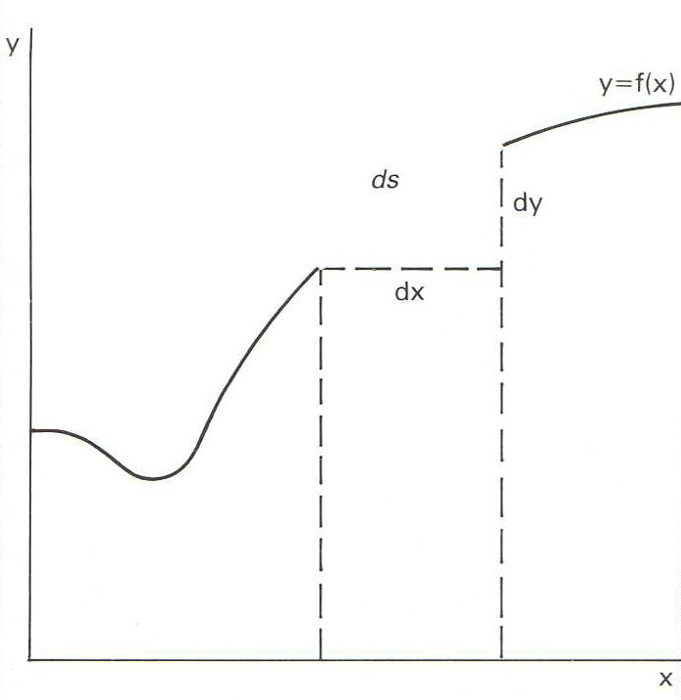
El principal problema que es planteja a propòsit d’un arc és el del càlcul de la seva llargada, és a dir, el de la rectificació de la corba. En el cas d’una circumferència de radi r, si l’arc α és mesurat en graus sexagesimals i val n graus, la seva llargada és s = rnπ/180. En la pràctica, el càlcul de la llargada d’un arc d’una corba qualsevol d’equació coneguda es redueix a una integració. Un arc infinitament petit ds, és assimilable a la seva corda i, si les coordenades dels seus extrems són x, y i x + dx, y + dy, en el cas d’una corba plana representada en coordenades cartesianes rectangulars per l’equació y = f(x), el teorema de Pitàgores