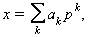Els coeficients ak són aleshores les xifres del nombre x en el sistema de numeració de base p. Per exemple, si fem p=10, l’expressió anterior porta al desenvolupament de les xifres del nombre x en el sistema de numeració decimal: 1525=1×103 + 5×102 + 2×101 + 5×1⁰. En el cas general d’un nombre enter p ≥2 qualsevol, obtenim el desenvolupament del nombre x en el sistema de numeració de base p. Els coeficients aksón les xifres de x en el sistema numèric posicional de base p. El nombre 2 és la base del sistema binari, el 8 la base del sistema octal, i el 16 la base del sistema hexadecimal, molt usats en informàtica. Per exemple, l’expressió del nombre 13 (decimal) en aquestes bases és, respectivament: 13)₂=1101 (ja que 13=1×23 + 1×22 + 0X21 + 1×2⁰), 13)₈=15 (13=1×81 + 5×8⁰) i 13)₁₆=d (ja que cal completar les xifres 0,1,2,...,9 amb sis lletres A,B,...,F, i 13=13×16⁰).
f
Matemàtiques
Nombre natural més gran que 1, p≥2, mitjançant el qual tot nombre natural x pot ésser expressat en forma d’un polinomi en p:
