Hom defineix l’operador diferència Δ, mitjançant l’expressió Δf(x) = f(x + ϖ) - f(x), i l’operador incremental E, definit per Eϖf(x)= f(x + ϖ) = f(x) + Δ f(x), de manera que E= 1+Δ. Les propietats d’aquests permeten d’assolir el resultat següent, dit teorema de Gregory: f(x + nϖ) = Enϖ f(x) = (1+Δ )n f(x), on, en l’última expressió, hom pot emprar la fórmula del binomi de Newton. Aquests operadors poden expressar les diferències dividides:
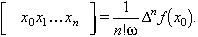
Hom pot obtenir una aproximació polinòmica a la funció f(x) amb la fórmula d’interpolació de Newton:
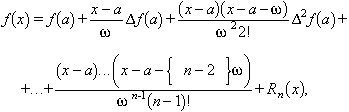
en la qual, si f(x) és n vegades diferenciable,
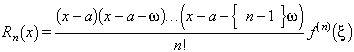
amb a a + (n-1)ω. Aquest valor permet de fitar l’error comès en l’aproximació. Hi ha mètodes amb els quals hom pot trobar aproximacions en forma de funcions racionals quan no n’hi ha prou amb les polinòmiques. Per a la diferenciació numèrica, la identificació formal de l’operació de derivació, representada per D, amb eϖD = f + Δ, permet d’obtenir l’expressió d’aquella, que resulta ésser ϖD = Δ-1/2 Δ2 + 1/3 Δ3+... Hom ha establert, també, una gran quantitat de fórmules per a determinar els resultats de la integració numèrica de funcions. Finalment, hi ha mètodes per a resoldre les equacions de diferències.