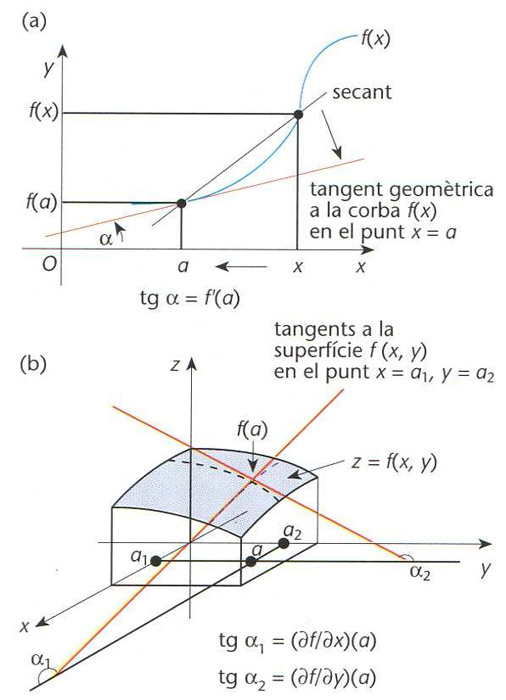
Quan aquest límit existeix, hom diu que la funció f és derivable en a, i el límit és notat per f´(a), (df/dx) (a) o Df(a), i hom l’anomena derivada de f en el punt a. Hom diu que f és derivable en un cert domini S si ho és a cada punt de S. Aleshores, la funció f´(x) que assigna a cada punt a∈S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f. Si f´(x) és, al seu torn, derivable en un cert domini T, hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´(x). Hom procedeix consecutivament per tal de definir les derivades d’ordre superior, f( n ). El conjunt de funcions derivables en un cert domini té estructura d’anell, i la derivada hi pot ésser entesa com un operador, anomenat derivació. Gràficament, hom pot interpretar f´(a) com la tangent trigonomètrica de l’angle que determina amb l’eix d’abscisses la tangent geomètrica, traçada en el punt d’abscissa a, de la gràfica de la funció f respecte a la seva variable x. El concepte de derivada és el fonament del càlcul diferencial i un dels més importants de l’anàlisi matemàtica. És de força utilitat per a estudiar les propietats d’una funció (determinació de màxims i mínims, concavitat i convexitat, etc).
f
Matemàtiques
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.