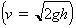Són fluids els líquids i els gasos, la diferència entre els quals està, des del punt de vista molecular, en la diferent concentració molecular, molt més gran en els líquids que en els gasos. Aquesta més alta concentració fa que en els líquids calgui matisar la noció de llibertat de moviment de les molècules (perquè no tenen obligació d’oscil·lar entorn d’unes posicions d’equilibri fixes, com passa en els sòlids) i, de passada, possibilita l’aparició d’una sèrie de fenòmens (tensió superficial, fenòmens de contacte i de capil·laritat) dels quals són responsables les forces intermoleculars residuals. Sovint hom defineix els fluids macroscòpicament, sense cap referència a l’estructura molecular; segons això, són fluids els sistemes materials en els quals és possible d’aconseguir un canvi de forma sense que calgui cap força, o sia, que, a diferència dels sòlids, en què per aconseguir un canvi de forma cal exercir-hi esforços tangencials, els fluids són els sistemes materials en els quals no es produeixen esforços tangencials. Cal tenir en compte que, bé que en realitat en els líquids i els gasos sempre hi ha uns petits esforços tangencials, generalment hom pot negligir-los; si aquests esforços són notables, hom parla de fluids viscosos. Atès que els únics esforços en els fluids ideals són normals, sempre és possible de definir, en cada punt d’un fluid, la pressió, que és la força que el fluid fa normalment a una superfície unitària col·locada en qualsevol orientació en el punt considerat. Els fluids poden ésser incompressibles (densitat independent de la pressió) o compressibles; els gasos són de la segona classe, mentre que pràcticament tots els líquids són de la primera. L’estudi quantitatiu de la dinàmica dels fluids és, en general, d’una gran complicació matemàtica. Quan el fluid és incompressible i es mou estacionàriament (la velocitat del fluid que passa per un punt fix de l’espai és constant en el transcurs del temps), hom obté, com a conseqüència de la segona llei de Newton, que la quantitat p + ρgh + 1/2 ρv2 (p essent la pressió, ρ la densitat, g l’acceleració de la gravetat, h l’alçada per damunt d’un nivell horitzontal arbitrari, i v la velocitat) es manté constant en els diferents punts del fluid ( principi de Bernoulli). La major part de les relacions quantitatives elementals vàlides per als fluids deriven d’aquest teorema: la llei de la hidroestàtica (fent v = 0), els principis de Pascal i d'Arquimedes, la fórmula de Torricelli