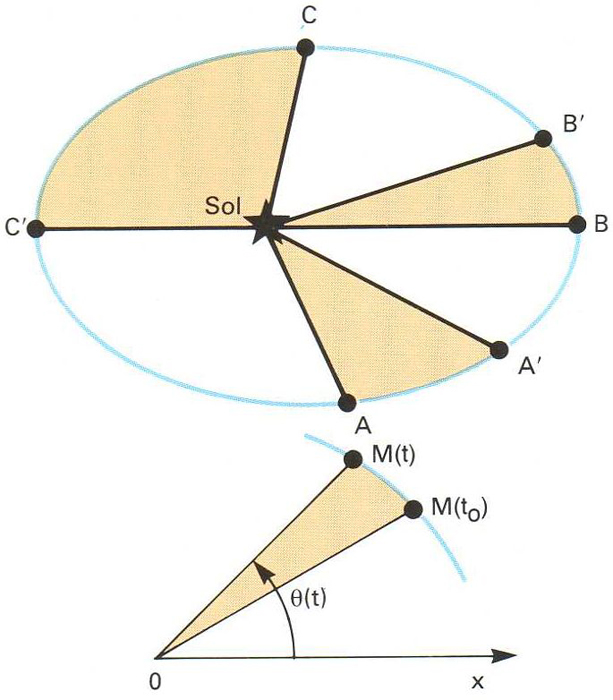
En astronomia, aquest teorema és aplicat a l’estudi del moviment d’un planeta respecte al Sol i és conegut com la segona de les tres lleis de Kepler. La demostració és obtinguda d’aplicar el teorema del moment angular al cas particular del moviment d’un punt material M
sotmès a un sistema de forces centrals que passen pel punt O
, respecte al qual hom obté els moments. Aquests moments tenen una resultant nul·la i, per tant, el moment angular L
és un vector constant perpendicular sempre als radis vectors, que descriuran com a conseqüència una trajectòria plana. Si hom considera la posició de M
en els temps t
i t
+ dt
, l’àrea descrita per r
en el temps dt
serà la del triangle OMM'
de valor dS = 1/2 Ldt/m
, com és fàcil de demostrar pel teorema del moment angular, i per tant proporcional només al temps com indica el teorema.
Si el punt material M
no és sotmès a forces centrals sinó a forces que sempre passen per un mateix eix, llavors el teorema de les àrees és aplicat a la projecció de la trajectòria sobre un pla perpedicular a l’eix.