Hom l’anomena logaritme de base b de n, i el representa per logbn = a. Les propietats fonamentals dels logaritmes són:
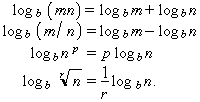
Els logaritmes neperians i els decimals són relacionats mitjançant l’anomenada fórmula del canvi de base, l’expressió de la qual és logen= log10n/log10e. En el cas dels logaritmes decimals, hom anomena característica la part entera del logaritme, mentre que la part decimal és la mantissa. La característica del logaritme d’un nombre n > 1 és el nombre de xifres, menys una, que n té abans de la coma; en el cas n taules logarítmiques prescindint de la coma que pugui tenir n. El procediment per a calcular mitjançant logaritmes el valor d’una expressió complicada consisteix a trobar, en primer lloc, el logaritme de l’expressió i cercar seguidament el seu antilogaritme.
La idea del logaritme com a instrument de càlcul és deguda a Jost Bürgi i, independentment, al seu contemporani John Napier, els quals el 1620 partiren d’un treball fet per Stifel el 1544. Els càlculs accessoris, cada vegada més complicats, en astronomia, trigonometria, comptabilitat, etc, exigien més facilitat i més exactitud. Bürgi fou el primer a elaborar les taules de logaritmes, però, en contra dels consells de Kepler, no les publicà; és per això que Napier ha tingut històricament molt més ressò, arran de la publicació, a Edimburg, del seu Mirifici logarithmorum canonis constructio (1619). Tant Bürgi com Napier s’aproparen al concepte de logaritme neperià, bé que cap d’ells no arribà a utilitzar la base e, fou H. Briggs qui proposà la utilització de la base 10.
Actualment les computadores han desplaçat els logaritmes com a estri de càlcul, bé que la funció logarítmica continua ocupant un lloc important, tant en la matemàtica pura com en l’aplicada.