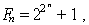El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5≤n≤17, Fn no és primer, i que d’altres nombres de Fermat, com F1945, F3310 i F6537 són descomponibles. El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats.
m
pl
Matemàtiques
(per a n = 1,2,3,...). 