Les fórmules de càlcul són: longitud de la circumferència, 2πR; àrea del cercle, πR2; àrea de l’esfera, 4πR2; volum de l’esfera, 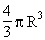
Pi és inicial del mot grec περιφέρεια (‘circumferència’). L’ús d’aquesta lletra grega per a designar la relació entre la longitud de la circumferència i el seu diàmetre es remunta solament al segle XVII, i es generalitzà a partir de la publicació de l’obra d’Euler Introductio in analysim infinitorum (el mateix Euler i J. Bernoulli usaren P i c, respectivament, com a símbol representatiu).
A Egipte s'havien fet aproximacions empíriques del valor de π. Fou Arquimedes qui proposà el primer mètode rigorós per a calcular π mitjançant aproximacions successives de la longitud d’una circumferència de diàmetre 1 (per excés i per defecte) en considerar polígons circumscrits i inscrits a la circumferència amb un nombre creixent de costats. Utilitzant polígons de 96 costats, Arquimedes arribà a limitar π entre 3 + 10/71 i 3 + 1/7 = 22/7 (de fet, l’error d’aproximar π per 22/7 és inferior a 0,002). Des de molts anys, es coneixia el valor 355/113 com a bona aproximació de π (les sis primeres xifres decimals coincideixen).
Al llarg de la història ha estat un problema central de la matemàtica, i de la ciència en general, el fet de cercar si π era un nombre racional (una fracció), ultra l’anomenat problema de la quadratura del cercle (construir a partir d’un cercle un quadrat d’àrea igual, amb regle i compàs). Fins al segle XVII aquests problemes reberen nombroses contribucions, totes elles insatisfactòries.
Lambert demostrà el 1761 que π és incommensurable (no racional, és a dir, irracional). Euler establí la relació de π i e (base dels logaritmes neperians) amb la sorprenent igualtat
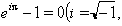
unitat imaginària); això permeté a Lindemann el 1882 demostrar que π era transcendent (no era solució de cap polinomi amb coeficients racionals, igualat a zero). Juntament amb altres resultats (com la teoria de Galois), fou resolt un vell problema: la quadratura del cercle i la representació de π amb regle i compàs són impossibles. Per al càlcul de π, Wallis usà el producte infinit
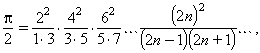
Euler emprà la sèrie
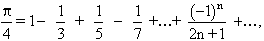
i Shanks, el 1874, calculà fins a 707 decimals (gravats en una sala del Palais de la Découverte, a París).
Amb les noves possibilitats computacionals, hom ha arribat a calcular els primers milers de decimals de π. Per exemple, el 1979 hom aconseguí de calcular els primers quinze milions de decimals de π. Els primers són π = 3,141 592 653 589 793 238 464 338 327..., però a la pràctica hom aproxima π per 3,1416, 3,14 o 355/113.