Les interseccions de les cares constitueixen les arestes, i les interseccions de les arestes, els vèrtexs. Un políedre és convex si qualsevol secció plana del políedre és un polígon convex. Un políedre és còncau si no és convex. Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats. Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars.
Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars: el tetràedre regular, l’hexàedre regular (o cub), l’octàedre regular, el dodecàedre regular i l’icosàedre regular, els quals tenen 4, 6, 8, 12 i 20 cares, respectivament.
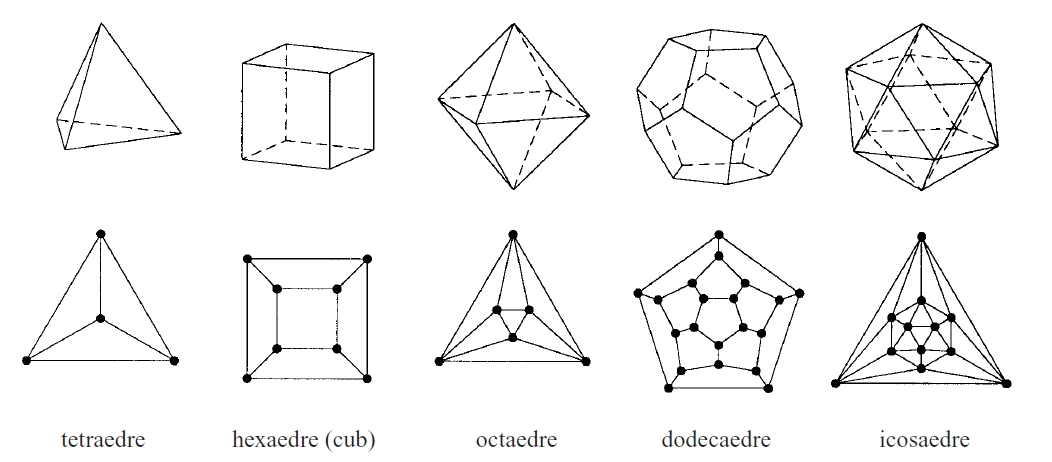
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
La relació d’Euler assegura que en un políedre el nombre de cares C més el de vèrtexs V és igual al nombre d’arestes A més dos, és a dir, C + V = A + 2.
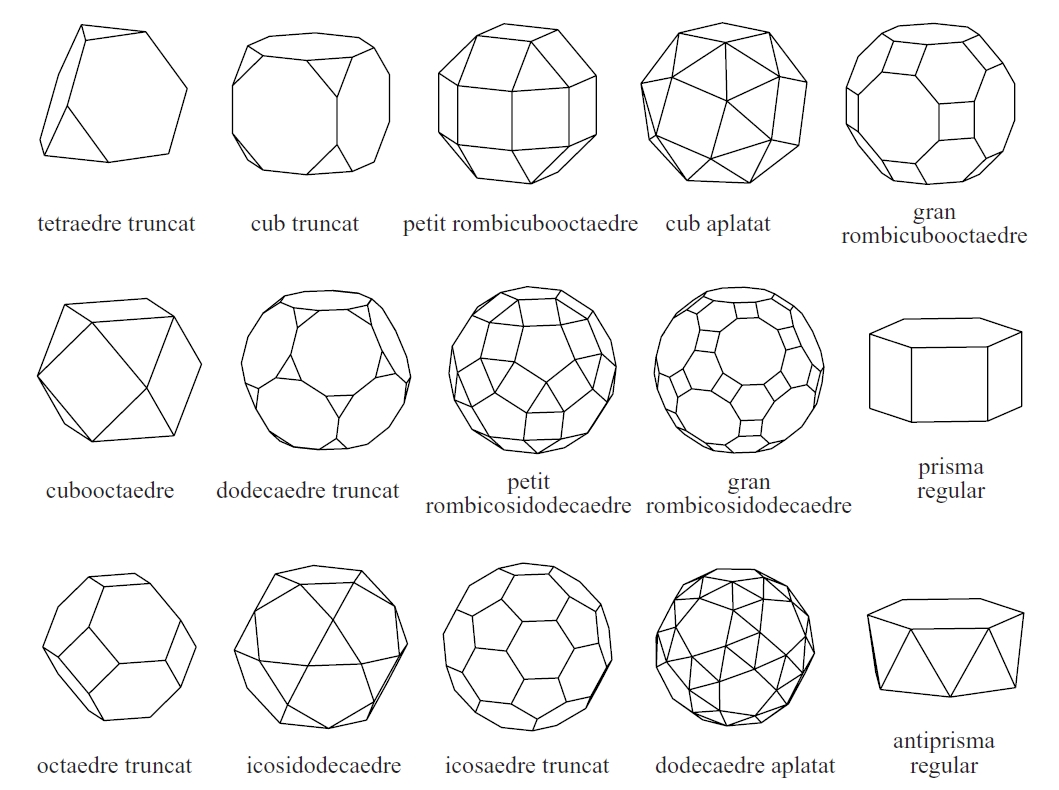
Els políedres semiregulars
© Fototeca.cat
Els políedres semiregulars són políedres convexos en què totes les cares són polígons regulars (no tots iguals) i tots els vèrtexs tenen el mateix nombre d’arestes incidents. A part d’infinits prismes i antiprismes, hi ha tretze tipus d’aquests políedres. Els centres de les seves cares determinen els tretze políedres de Catalan.
El políedres són irregulars quan no tenen unes condicions d’ordre o de simetria.