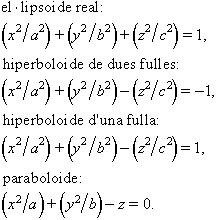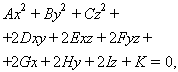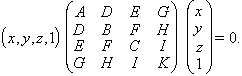Si notem la primera matriu (associada a les coordenades d’un punt) per α, i la segona (formada pels coeficients de la quàdrica) per β, aleshores l’anterior expressió pot escriure's com αtβα ═ 0, on αtés la matriu transposada de α. Dos punts M0 i M1 són dits conjugats respecte a una quàdrica quan llurs matrius satisfan αt0βα1 = 0. Un pla és anomenat pla polar d’un punt respecte a una quàdrica quan és format pels punts conjugats del punt considerat. Hom anomena centre de la quàdrica qualsevol punt conjugat de tots els punts de l’infinit, i plans diametrals, els plans polars dels punts de l’infinit.
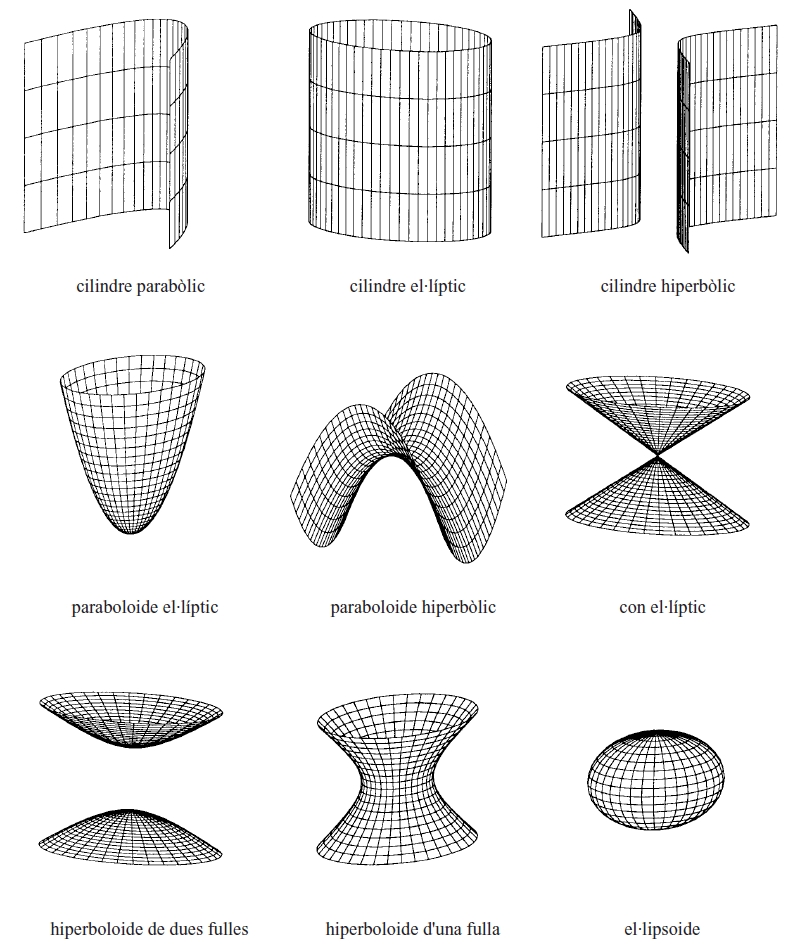
quàdriques
Hom classifica les quàdriques d’acord amb els valors dels diferents paràmetres. En coordenades cartesianes, i referides a llurs eixos de simetria, les equacions de les quàdriques més notables són