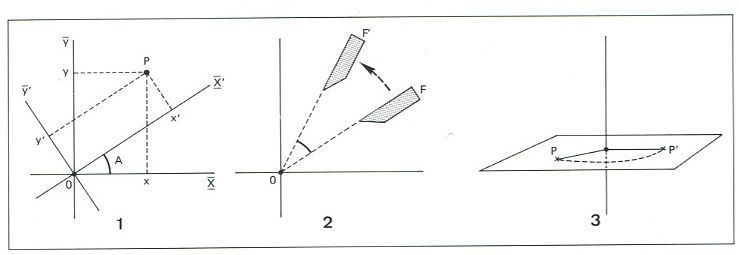
En el pla hom considera la rotació al voltant d’un punt (fix) que correspon a moviments rígids circulars de centre al punt donat. En l’espai hom considera la rotació al voltant d’una línia, en la qual qualsevol punt d’una figura es mou en sentit circular al voltant de la línia donada (eix de rotació), en un pla perpendicular a aquesta i que passa pel punt donat. Una rotació d’eixos correspon a una rotació que deixa fix l’origen de coordenades. Aquestes rotacions permeten de passar d’un sistema de referència a un altre que pot ésser més adequat per a l’estudi d’un problema geomètric concret (així, per exemple, l’equació d’una paràbola o d’una el·lipse se simplifica si hom pren una referència que contingui els elements de simetria d’aquestes figures). En el pla, les coordenades (x',y') d’un punt P respecte a un sistema de referència obtingut en girar un angle α, un sistema inicial on el punt P tenia coordenades (x,y) mantenen la relació següent
x = x' cos α - y' sin α
y = x' sin α + y' cos α,
que pot ésser expressada en forma matricial per
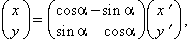
on la primera matriu del segon terme és la matriu de rotació. Les equacions corresponents a rotacions d’eixos en l’espai són:
x = x' cos α1 + y' cos α2 + z' cos α3,
y = x' cos β1 + y' cos β2 + z' cos β3,
z = x' cos γ1 + y' cos γ2 + z' cos γ3,
que en forma matricial és expressat per
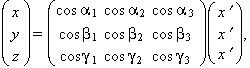
on α,β,γ són els angles directors del nou sistema de referència respecte a l’antic.