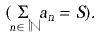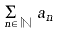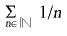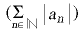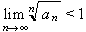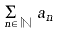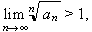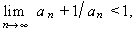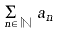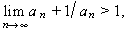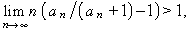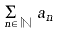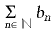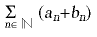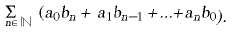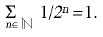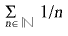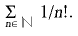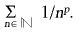La teoria de sèries s’ocupa especialment del cas infinit numerable. Així, una sèrie és donada per una successió de nombres a₁ , a₂ , ..., an , ... (on an és dit terme general n -èsim de la successió) i una successió associada formada per les sumes parcials a₁, a₁ + a₂, a₁ + a₂ + a₃, ..., a₁ + ... + an , ... Simbòlicament hom representa una sèrie per
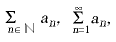
, o bé a₁ + a₂ ... + an + ... Si la successió de sumes parcials és convergent cap a un límit S, hom diu que la sèrie és convergent i de suma S
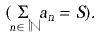. En cas de no existir aquest límit, la sèrie és dita divergent. Una sèrie és dita positiva o negativa segons que tots els nombres que la determinen siguin positius i negatius. Una sèrie és anomenada creixent o decreixent (o també, ascendent o descendent) si els nombres determinats de la sèrie formen respectivament una successió creixent o decreixent de valors. Tota sèrie creixent és necessàriament divergent. Si una sèrie
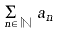és convergent, aleshores la successió (an) té límit zero, però el recíproc no és generalment cert. Per exemple,
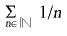divergeix i, per contra, 1/ n tendeix a zero. Una sèrie és dita alternada si els signes dels termes de la successió determinant són alternativament positius i negatius. Una sèrie alternada és convergent si i només si el seu terme general tendeix a zero. Una sèrie és absolutament convergent si la sèrie dels valors absoluts dels termes de la sèrie
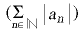és una sèrie convergent. Per a sèries de termes positius hi ha diferents criteris de convergència; els més coneguts són el de Cauchy, segons el qual si
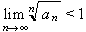aleshores
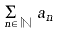és convergent, i si
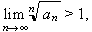, la sèrie és divergent; el de D’Alembert, que afirma que si
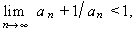, aleshores
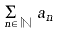convergeix, i si
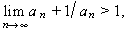, la sèrie divergeix; el de Raabe que diu que si
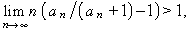, la sèrie convergeix, i si el límit és menor que 1, aleshores divergeix. La suma de dues sèries
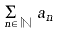i
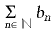és definida per la sèrie
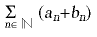producte d’ambdues mitjançant
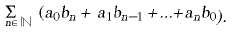. Si dues sèries són absolutament convergents, la seva suma i el seu producte també ho són. Una sèrie és anomenada aritmètica o geomètrica, segons que els seus termes formin respectivament una progressió aritmètica o geomètrica. Una sèrie geomètrica a + ar + ar2 + ar3 + ... + ar n-1, amb raó r menor que 1, és convergent i té per suma a / (1— r). Per exemple,
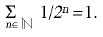1/2 n = 1. Una sèrie és dita harmònica si els recíprocs dels seus termes formen una sèrie aritmètica. Per exemple, la sèrie
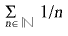és harmònica. La sèrie factorial és
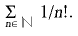. Les sèries
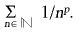, que tenen un especial interès estadístic, són convergents per a p major que 1 i divergeixen per a p menor que 1 o igual a 1. Cal remarcar que amb els mateixos termes numèrics hom pot, alterant-ne l’ordre, fer una altra sèrie, dita reordenada de l’anterior. Si una sèrie és absolutament convergent, totes les seves reordenacions també ho són i tenen la mateixa suma. Així, la teoria de sèries numèriques permet de resoldre el problema de sumar una infinitat de termes com un pas al límit de sumes finites.