Cal distingir sempre el símbol del concepte. Així, el nombre dos (concepte) pot ésser representat per símbols diferents: 2, II, ╫, etc.
Principals símbols
| símbols emprats en teoria de conjunts | |
| ∈ | pertany a |
| ∉ | no pertany a |
| = | igual a |
| ≠ | diferent |
| ⊂ | inclusió, és inclòs en |
| ⊄ | no és inclòs en |
| ⋂ | intersecció |
| ⋃ | reunió |
| − | diferència |
| ∁ , − , ∽ | complementari |
| ∆ | diferència simètrica |
| → | aplicació, funció |
| ≃ | coordinable, bijectiu |
| x | producte cartesià |
| {} | singletons |
| [] | claudàtors |
| ∅ | conjunt buit |
| ℕ | nombres naturals |
| ℤ | nombres enters |
| ℚ | nombres racionals |
| ℝ | nombres reals |
| ℂ | nombres complexos |
| símbols emprats en lògica | |
| ⋁ | o |
| ⋀ | i |
| − , ¬ | no |
| ⟹ | implica |
| ⟺ | si i solament si, equivalent |
| Ǝ | existeix |
| ∀ | per a tot |
| ≗ | per definició igual a |
| símbols emprats en trigonometria i geometria | |
| aº | a graus d’angle |
| a' | a minuts d’angle |
| a'' | a segons d’angle |
| sin | sinus |
| cos | cosinus |
| sec | secant |
| cosec | cosecant |
| ┴ | perpendicular |
| ∥ | paral·lel |
| cdg | centre de gravetat |
| tg , tan | tangent |
| cotg , cotan | cotangent |
| símbols emprats en aritmètica | |
| + | més, positiu |
| − | menys, negatiu |
| = | igual |
| ≡ | idèntic a, congruent amb aproximadament igual a |
| ≥ , ≧ | major o igual que |
| ≤ , ≦ | menor o igual que |
| > | major que |
| < | menor que |
| () | parèntesis |
| {} | claus |
| [] | gafets |
| ∆ | increment |
| ∥ | valor absolut |
| a b , a · b , a x b | a vegades b, a per b, a multiplicat per b |
x1/n , 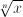 |
arrel enèsima de x |
x 1/2 , 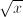 |
arrel quadrada de x |
| ∞ | infinit |