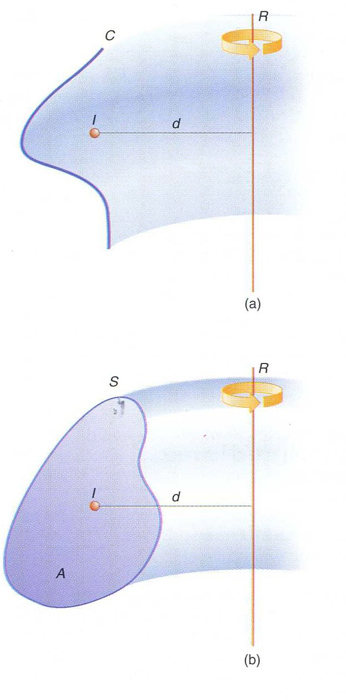
Segons el primer teorema de Guldin, donada una corba plana C, de longitud l, que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2πdl, on d és la distància des del centre de massa I de la corba a la recta R (en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica; en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material).
El segon teorema de Guldin afirma que, donada una superfície plana S, d’àrea A, que gira al voltant d’una recta R del seu pla, la qual no talla, el volum V del sòlid de revolució que genera és V = 2πdA, on d és la distància des del centre de massa I de la superfície a la recta R (el centre de massa és calculat de la mateixa forma que en el primer teorema).